Frontières de la psychologie

La décroissance entraîne-t-elle l’oubli ? Pour la mémoire à long terme, on s’accorde généralement à répondre par la négative (par exemple, McGeoch, 1932). Pour la mémoire à plus court terme, cependant, le débat se poursuit (par exemple, Altmann et Gray, 2008 ; Lewandowsky et al., 2009). Cette question a des implications théoriques importantes, car l’affirmation selon laquelle l’oubli diffère selon les échelles de temps est au cœur des arguments contre les modèles de mémoire qui nient l’utilité de la distinction entre la mémoire à court terme et la mémoire à long terme (par exemple, Brown et al., 2007). Nous abordons ici deux questions restantes. La première concerne les données empiriques. Bien que de nombreux résultats considérés comme des preuves de la désintégration aient été expliqués par des comptes alternatifs (par exemple, en termes d’interférence : Neath et Brown, 2006 ; Brown et al., 2007), il a été soutenu que l’oubli démontré par Baddeley et Scott (1971) ne peut être expliqué sans avoir recours à la désintégration des traces. En effet, Nairne (2003, p. 429) a déclaré que  » les conclusions de Baddeley et Scott (1971) ont largement dominé le domaine au cours des trois dernières décennies « . Ici, nous soutenons qu’une explication basée sur l’interférence, initialement rejetée par Baddeley et Scott, peut en fait rendre compte de leurs données. La deuxième question est conceptuelle et concerne l’équivalence possible des modèles de mémoire à décroissance et à non décroissance.

Les résultats de Baddeley et Scott (1971)

Dans une tâche typique de Brown-Peterson (Brown, 1958 ; Peterson et Peterson, 1959), les sujets visualisent trois éléments (généralement des consonnes) et, après un délai de 3 à 30 s, tentent de les rappeler dans l’ordre. La répétition est empêchée pendant la rétention, et l’oubli se produit avec le temps. Keppel et Underwood (1962), cependant, n’ont observé aucune différence de performance dans les diverses conditions de délai lors du premier essai d’une tâche de Brown-Peterson. Par exemple, dans leur expérience 2, la performance au premier essai était identique, que la période de distraction dure 3, 9 ou 18 secondes (pour une analyse, voir Surprenant et Neath, 2009a). Ils en ont conclu que l’interférence, plutôt que la dégradation des traces, était responsable de l’oubli à court terme. Conformément à la vision de l’interférence, la performance a diminué au fil des essais.

Baddeley et Scott (1971) ont toutefois suggéré que les données de Keppel et Underwood (1962) souffraient d’effets de plafond qui auraient pu masquer l’oubli. Ils se sont donc penchés sur l’oubli du premier essai lorsque les effets de plafond étaient absents. Dans l’expérience 1, 152 sujets ont entendu une liste unique de cinq éléments numériques dans un ordre aléatoire, dont ils se sont souvenus après 3, 30, 60 ou 120 s. Pendant le délai, les sujets ont écrit des lettres qui étaient lues à haute voix par l’expérimentateur. Les résultats (points de données, panneau gauche de la figure 1) comprenaient des preuves claires d’oubli entre 3 et 30 s lors du premier (c’est-à-dire le seul) essai.

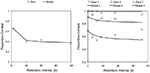
Figure 1. Les points de données montrent la proportion d’éléments correctement rappelés dans l’expérience 1 de Baddeley et Scott (1971) (panneau gauche) et la proportion d’éléments correctement rappelés à partir de listes de trois, cinq et sept éléments dans l’expérience 2 (panneau droit) en fonction du délai. Les lignes solides montrent l’ajustement de SIMPLE (voir le texte pour plus de détails).

L’expérience 2 a exploré davantage l’oubli d’un seul essai. Quatre cent vingt-quatre sujets ont rappelé des listes de chiffres de trois, cinq ou sept éléments après 0, 3, 6, 9, 18 ou 36 s. La tâche distractive consistait à nouveau à écrire des lettres. Les résultats sont présentés (sous forme de points de données) dans le panneau de droite de la figure 1. Baddeley et Scott(1971, p. 282) ont inclus dans leur analyse des données provenant d’autres études et ont noté que sur l’ensemble des études, y compris la leur, « l’oubli s’approche de l’asymptote dans un délai d’environ 5 s. »

Les sujets n’ont reçu qu’un seul essai, empêchant toute interférence proactive, et pourtant l’oubli s’est produit. D’autres sources possibles d’interférence ont été envisagées et écartées. Tout d’abord, l’interférence rétroactive de la tâche de distraction a été jugée peu probable en raison de l’absence de preuve que les lettres et les chiffres interfèrent mutuellement (Wickens et al., 1963). Deuxièmement, l’interférence intraséquence – les éléments de la liste interférant les uns avec les autres – a été exclue car une telle interférence devrait entraîner un oubli plus rapide pour les listes plus longues (voir Melton, 1963), ce qui n’a pas été observé. Baddeley et Scott (1971) ont donc considéré leurs résultats comme une preuve de l’existence d’une composante de mémoire primaire qui disparaît en 5 secondes environ. Depuis sa publication, l’étude a été abondamment citée comme preuve contre une explication des données par l’interférence et comme preuve de la décroissance ; il existe peu d’autres explications de ces données particulières et aucune tentative systématique de modélisation des données1. Un modèle sans trace de désintégration peut-il expliquer les données ? Ici, nous appliquons un modèle de distinction temporelle, la mémoire, la perception et l’apprentissage indépendants de l’échelle (SIMPLE ; Neath et Brown, 2006 ; Brown et al, 2007), aux résultats rapportés par Baddeley et Scott.

Preuves d’interférence

SIMPLE – scale independent memory, perception, and learning a été décrit en détail ailleurs (par exemple, Neath et Brown, 2006 ; Brown et al., 2007) ; ici, nous nous concentrons sur les aspects pertinents pour la simulation actuelle. La mémoire est conçue comme une tâche de discrimination : les éléments sont représentés comme des emplacements le long d’une ou plusieurs dimensions de l’espace psychologique et, en général, les éléments ayant moins de voisins proches sur les dimensions pertinentes au moment de la récupération seront plus susceptibles d’être rappelés que les éléments ayant plus de voisins proches. Selon SIMPLE, les éléments non liés dans les tâches de mémoire épisodique sont représentés principalement ou uniquement selon une dimension temporelle2. Le point zéro est le moment où l’élément est récupéré, et la valeur de chaque élément est le temps écoulé depuis la présentation, par rapport au moment de la récupération.

Dans l’expérience 1 de Baddeley et Scott (1971), le rythme de présentation était d’un élément par seconde, et par conséquent, les valeurs temporelles initiales à la fin de la présentation seront respectivement de 5, 4, 3, 2 et 1 pour les éléments 1 à 5. À ces valeurs s’ajoute la durée de l’intervalle de rétention (3, 30, 60 ou 120 s, selon la condition). On suppose que le rappel prend du temps ; nous avons supposé que le rappel de chaque item prend 1 s. Les valeurs résultantes sont transformées logarithmiquement, et la probabilité de rappel d’un élément particulier dépend de son caractère distinctif local.

La similarité, ηi,j, entre deux représentations de la mémoire temporelle transformées logarithmiquement, LTi et LTj, est donnée par Eq. 1:

Le principal paramètre libre dans SIMPLE est c : des valeurs plus élevées de c correspondent à une plus grande distinctivité et donc à une moindre influence des éléments plus éloignés.

La discriminabilité de l’élément i, Di, lorsqu’on lui donne l’indice (localisation temporelle) du stimulus j, Cj, est donnée par l’équation 2, dans laquelle n est le nombre d’éléments dans l’ensemble :

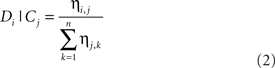
Les erreurs d’omission sont possibles grâce à l’équation. 3, qui montre la probabilité de rappel, Ri, en fonction de la discriminabilité:

Paramètre t est le seuil et le paramètre s peut être interprété comme le caractère bruyant du seuil. Ce qui précède est la même manière dont SIMPLE a été appliqué aux données de rappel en série dans des démonstrations antérieures (voir Neath et Brown, 2006 ; Brown et al., 2007).

Il y a donc trois paramètres libres. Avec c = 3,248, s = 8,253 et t = 0,269, SIMPLE montre un oubli clair (les lignes dans le panneau gauche de la figure 1) et produit adéquatement le même modèle observé par Baddeley et Scott (1971) dans leur expérience 1 (R2 = 0,954). Ainsi, bien qu’il n’intègre pas la décroissance des traces, SIMPLE rend compte des données de l’expérience 1 de Baddeley et Scott exactement de la même manière qu’il le fait pour le rappel immédiat en série en général.

Pourquoi la performance dans le modèle diminue-t-elle entre 3 et 30 s, mais s’asymptote ensuite efficacement ? La clé est ce que Brown et al. (2007) appellent la compression wébérienne. Les valeurs temporelles originales subissent une transformation logarithmique, qui condense davantage les grandes valeurs que les petites. Par conséquent, il y a moins de différence lorsqu’on compare le caractère distinctif des éléments après un délai de 30 et 60 s que lorsqu’on compare le caractère distinctif des éléments après un délai de 0 et 30 s.

La même procédure de base a été suivie pour ajuster les données de l’expérience 2 de Baddeley et Scott (1971). Les paramètres ont été fixés à c = 0,547, s = 23,131, et t = 0,139 pour les trois longueurs de liste et les six délais. Les résultats sont présentés sous forme de lignes dans le panneau droit de la figure 1 (R2 = 0,937). L’oubli différentiel entre les listes de trois, cinq et sept éléments s’explique entièrement par la présence d’éléments supplémentaires dans la liste, ce qu’on appelle l’interférence intraséquentielle.

Discussion

Le compte rendu dominant des données de Baddeley et Scott (1971) est qu’il offre un soutien pour un compte multi-système de la mémoire dans lequel la mémoire primaire (ou à court terme ou de travail) se désintègre en quelques secondes et le souvenir à plus long terme est soutenu par un deuxième système de mémoire (voir Nairne, 2003). La logique sous-jacente était que, puisque toutes les sources d’interférence étaient minimisées ou éliminées, tout oubli observé devait être dû à la décroissance.

Baddeley et Scott (1971) ont exclu l’interférence intraséquence comme explication parce qu’ils se sont concentrés sur le compte de Melton (1963) de l’interférence intraséquence, qui prédit effectivement un oubli plus rapide pour les listes plus longues. En revanche, SIMPLE ne fait pas cette prédiction parce qu’il s’agit d’un modèle de distinction locale : la quantité d’interférence pour un élément donné est plus affectée par les voisins proches, et donc l’extension de la longueur de la liste ne garantit pas nécessairement un oubli plus rapide. Ainsi, il est possible de rendre compte des données rapportées par Baddeley et Scott sans invoquer ni la décroissance ni deux systèmes de mémoire distincts, et au lieu de cela, en invoquant le même compte d’interférence utilisé pour expliquer les données d’autres paradigmes (voir Surprenant et Neath, 2009b).

Equivalence entre les modèles de décroissance et d’interférence?

Nous avons démontré qu’un modèle sans décroissance s’adapte aux résultats empiriques qui ont longtemps été considérés comme des preuves de la décroissance. On pourrait toutefois faire valoir que le modèle SIMPLE peut être interprété comme un modèle de haut niveau qui ne précise pas les processus clés sous-jacents (c’est-à-dire la décroissance par rapport à l’interférence)3. Essentiellement, cette accusation fait valoir que le concept de « distinctivité relative », qui est au cœur du comportement de SIMPLE, pourrait être mis en œuvre par des mécanismes de désintégration des traces. Nous considérons cela dans le contexte d’un modèle de décroissance basé sur le temps d’Anderson et al. (1998), qui utilise le cadre ACT-R.

Dans le modèle ABLM, l’activation de base d’une occurrence unique d’un chunk en mémoire décroît comme une fonction logarithmique du temps écoulé. Ainsi, les activations de base des éléments se situent dans les mêmes relations les unes par rapport aux autres que les distances temporelles transformées logarithmiquement utilisées par SIMPLE et pourraient, au moins algébriquement, être utilisées dans le même but, de la même manière que les dimensions autres que le temps ont été utilisées avec SIMPLE (voir le chapitre 8 de Surprenant et Neath, 2009b). Plus précisément, si la confusabilité des éléments en mémoire était liée aux différences dans leurs niveaux d’activations de base décomposées, et que la probabilité de se souvenir d’un élément donné était inversement liée à sa confusabilité sommée avec tous les autres éléments, alors un mécanisme de décomposition des traces pourrait être utilisé pour mettre en œuvre les mêmes calculs de distinctivité temporelle que ceux que suppose SIMPLE4.

L’interprétation psychologique de ce type de compte, cependant, semble quelque peu contre-intuitive. L’interprétation de la théorie de la décroissance prétend que ce qui rend un élément temporellement distant difficile à mémoriser n’est pas son faible niveau d’activation, mais plutôt le fait qu’il y a beaucoup d’autres éléments avec des niveaux d’activation tout aussi faibles. En effet, dans un tel modèle, il n’y aurait aucune relation directe entre le niveau d’activation d’un élément et la probabilité de se souvenir de cet élément ; au contraire, tout ce qui compterait serait la similarité entre le niveau d’activation de l’élément et les niveaux d’activation d’autres éléments. Il serait donc contre nature de dire que l’oubli se produit en raison de la décroissance.

Nous supposons qu’un mécanisme plausible d’oubli basé sur la décroissance fait au moins deux affirmations : premièrement, que les activations diminuent avec le temps et, deuxièmement, que la probabilité de récupération reflète d’une certaine manière le niveau absolu d’activation. Une fois qu’il est supposé que les éléments qui se sont dégradés davantage peuvent néanmoins être mieux récupérés, le modèle cesse d’être un modèle de dégradation des traces dans toute utilisation sensée. Ainsi, bien que le compte SIMPLE soit couché à un haut niveau de description et pourrait être mis en œuvre de plus d’une façon, nous suggérons qu’une interprétation en termes de dégradation des traces étire le sens de  » dégradation des traces  » au-delà de l’usage normal.

En résumé, nous avons fait valoir que les données classiques de Baddeley et Scott (1971), qui ont fréquemment été prises comme preuve de la décroissance, sont plus naturellement expliquées en termes de distinctivité temporelle.

Remerciements

Ce travail a été soutenu, en partie, par une subvention du CRSNG à Ian Neath et par la subvention RES-062-23-2462 du Economic and Social Research Council (UK) à Gordon D. A. Brown. Le code MATLAB pour les simulations est disponible à http://memory.psych.mun.ca/models/simple/misc/baddeley_1971.shtml ou auprès du premier auteur.

Notes de bas de page

Surprenant, A. M., Neath, I., et Brown, G. D. A. (2006). Modélisation des différences liées à l’âge dans la mémoire immédiate en utilisant SIMPLE. J. Mem. Lang. 55, 572-586.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text