La leçon 4 : Multiplication et division de fractions
/fr/fractions/addition et soustraction de fractions/contenu/
Multiplication de fractions
Une fraction est une partie d’un tout. Dans la dernière leçon, vous avez appris à additionner et à soustraire des fractions. Mais ce n’est pas le seul type de mathématiques que vous pouvez faire avec des fractions. Il y a des moments où il sera utile de multiplier des fractions aussi.
Cliquez à travers le diaporama pour apprendre à écrire un problème de multiplication avec des fractions.
-

Mettons en place un exemple de multiplication avec des fractions. Supposons que vous buvez 2/4 d’un pot de café chaque matin.
-

Mais votre médecin vient de vous dire que vous devez réduire de moitié votre consommation de café.
-
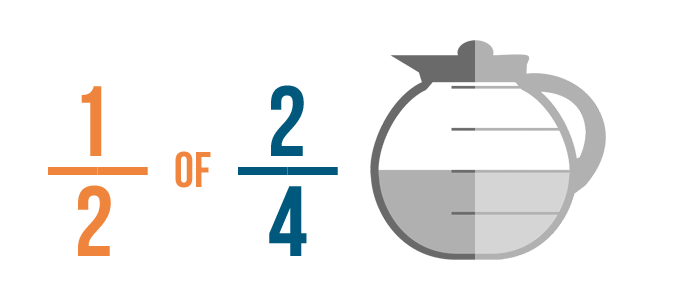
Maintenant, vous devez calculer combien représente 1/2 de 2/4 d’un pot de café.
-
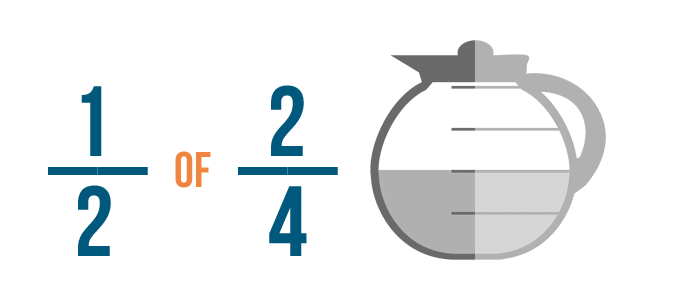
Cela ne ressemble peut-être pas à un problème de multiplication. Mais lorsque vous voyez le mot de avec des fractions, cela signifie que vous devez multiplier.
-
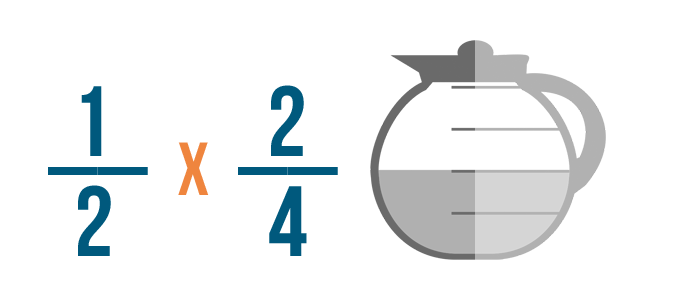
Pour mettre en place l’exemple, nous allons simplement remplacer le mot de par un signe de multiplication.
-
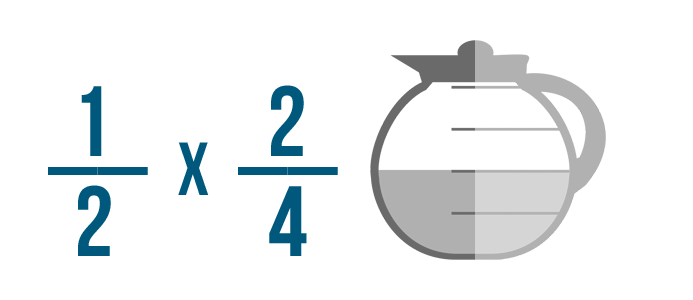
Maintenant notre exemple est prêt à être résolu.
-
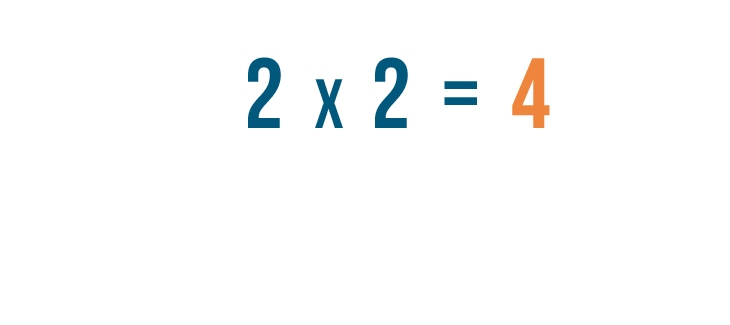
Contrairement à la multiplication ordinaire, qui vous donne un nombre plus grand….
-
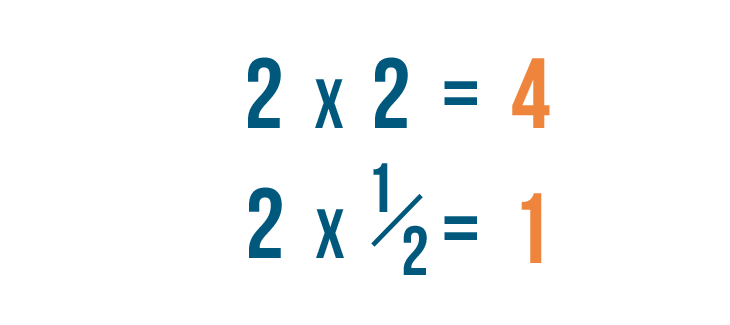
Contrairement à la multiplication régulière, qui vous donne un nombre plus grand…la multiplication de fractions vous donnera généralement un nombre plus petit.
-
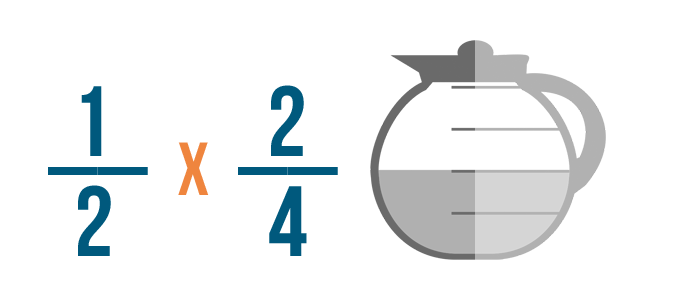
Donc, quand on multiplie 1/2 fois 2/4.
-
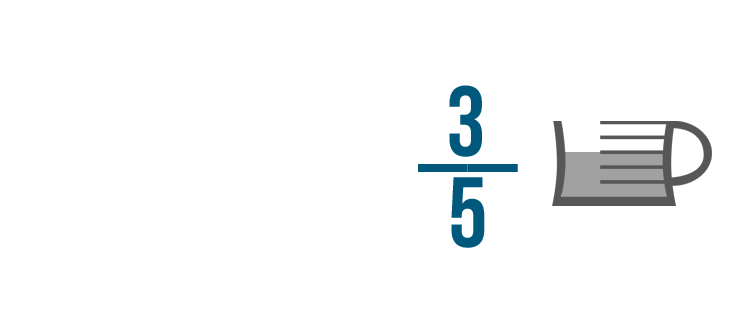
Voici un autre exemple. Disons que vous avez 3/5 d’une tasse de garniture au chocolat.
-
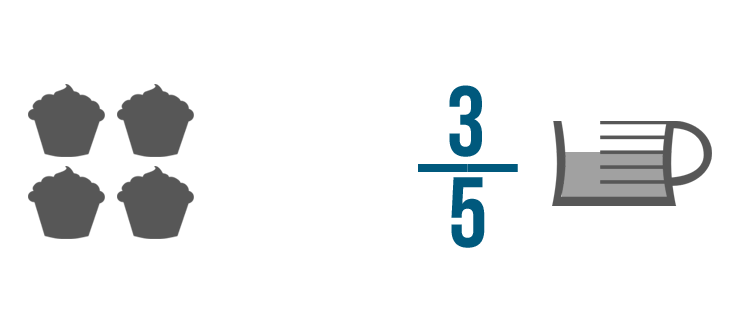
Vous voulez mettre une quantité égale de garniture dans chacun de ces 4 cupcakes.
-
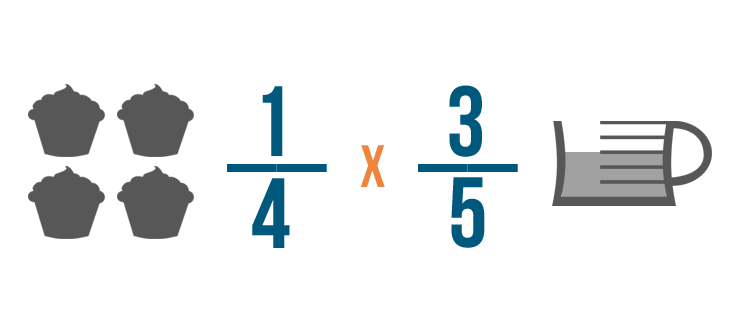
Comme nous l’avons fait précédemment, nous allons changer le mot de en signe de multiplication.
-
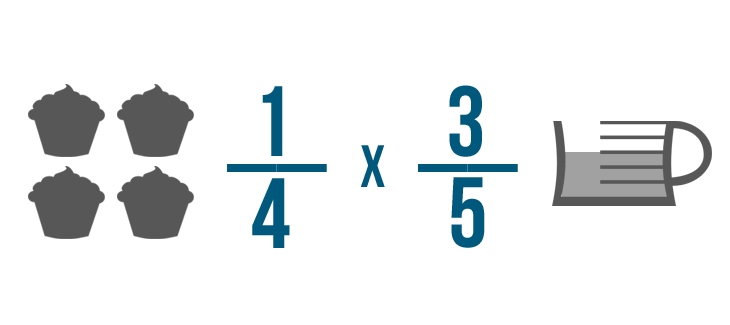
Et maintenant nos fractions sont prêtes à être multipliées.


Donc, lorsque nous multiplions 1/2 fois 2/4… notre réponse sera plus petite que 2/4.
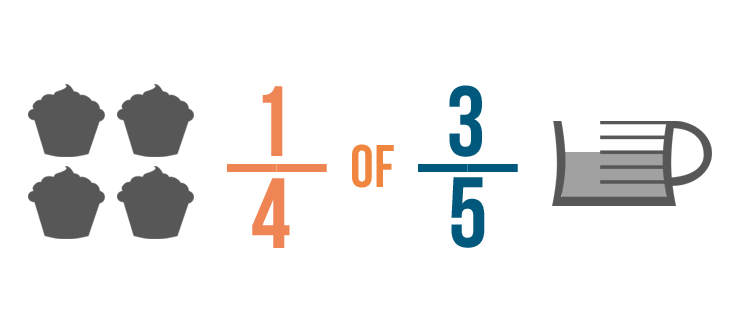
Vous pourriez dire que vous voulez mettre 1/4 de 3/5 de tasse de garniture dans chaque cupcake.
Essayez ça!
Essayez de mettre en place le problème de multiplication ci-dessous. Ne vous souciez pas encore de le résoudre !
Une recette demande 2/3 de tasse de lait. Vous voulez couper la recette en deux.

Note : bien que notre exemple indique que la bonne réponse est 2/3 x 1/2, rappelez-vous qu’avec la multiplication l’ordre n’a pas d’importance. 1/2 x 2/3 serait également correct.
Résoudre des problèmes de multiplication avec des fractions
Maintenant que nous savons comment établir des problèmes de multiplication avec des fractions, exerçons-nous à en résoudre quelques-uns. Si vous vous sentez à l’aise pour multiplier des nombres entiers, vous êtes prêt à multiplier des fractions.
Cliquez sur le diaporama pour apprendre à multiplier deux fractions.
-
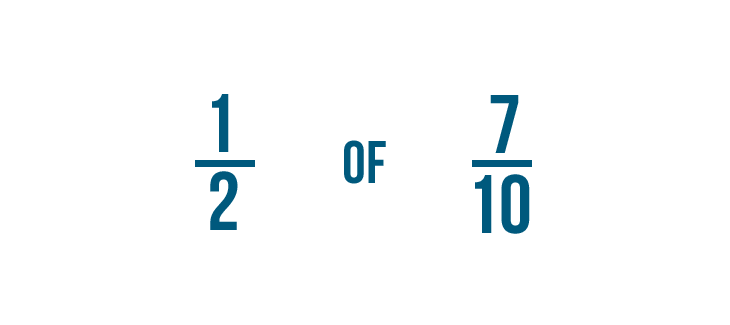
Multiplions pour trouver 1/2 de 7/10.
-
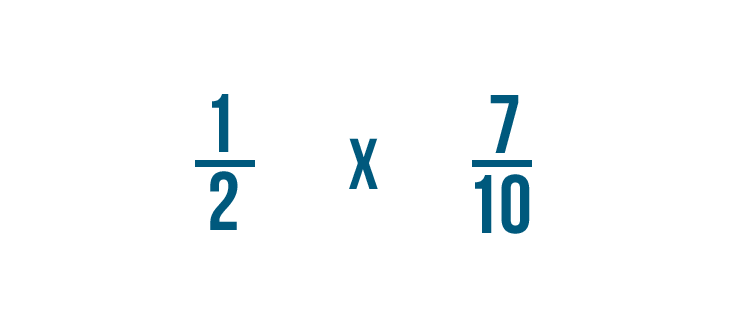
Comme nous l’avons fait précédemment, nous allons remplacer le mot de par un signe de multiplication. Maintenant, nous sommes prêts à multiplier.
-
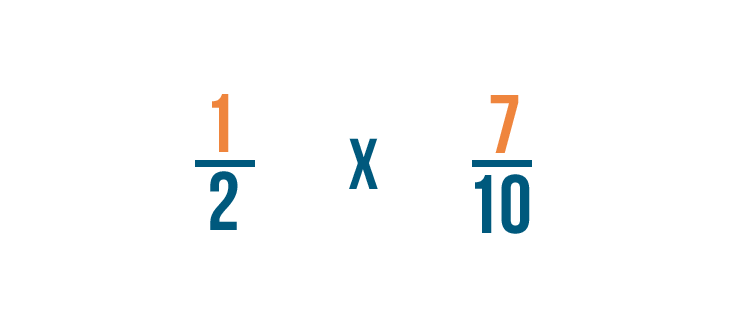
D’abord, nous allons multiplier les numérateurs : 1 et 7.
-
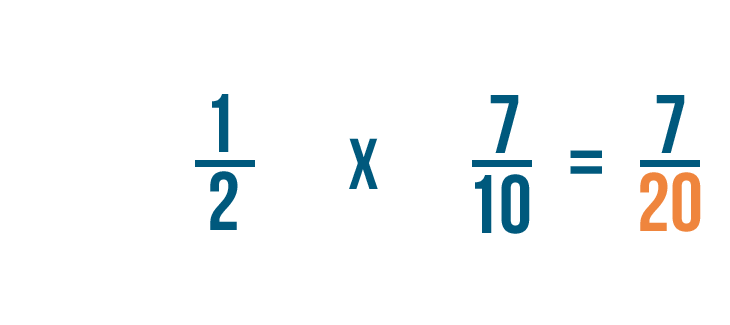
2 fois 10 égale 20, on va donc écrire 20 à droite des dénominateurs.
-
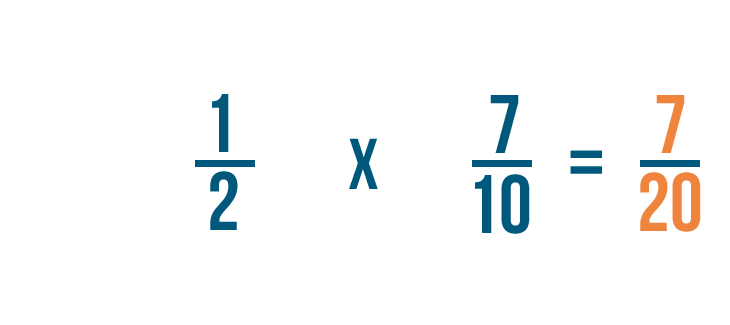
Nous pourrions aussi dire que 1/2 de 7/10 est égal à 7/20.
-
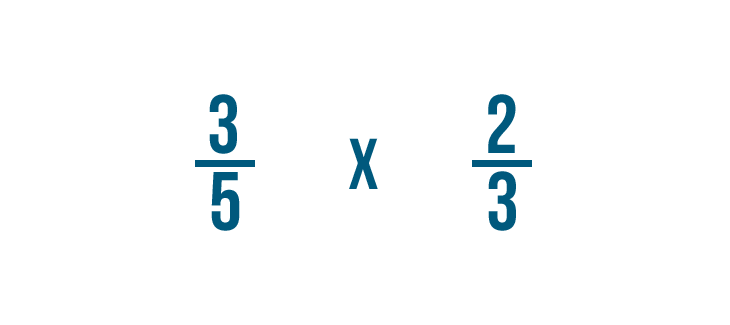
Tentons un autre exemple : 3/5 fois 2/3.
-
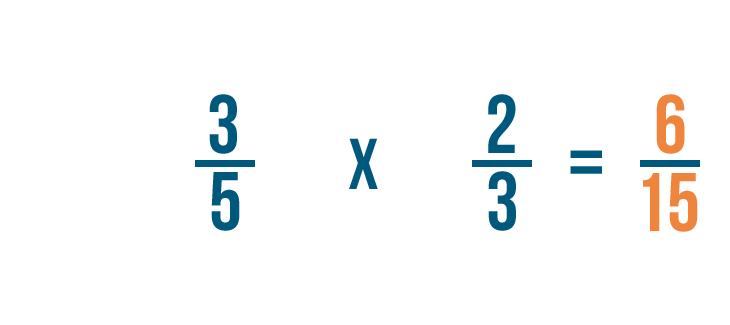
Donc 3/5 fois 2/3 est égal à 6/15.

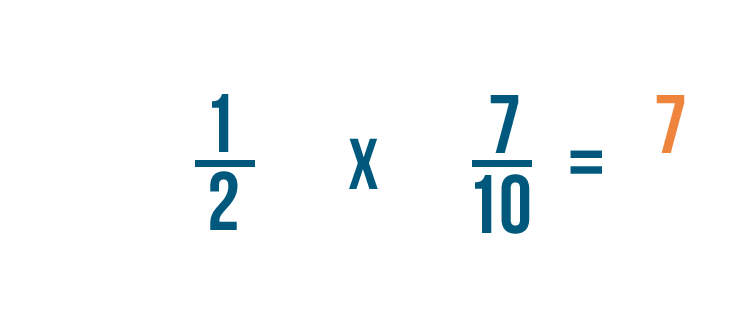
1 fois 7 égale 7, nous allons donc écrire 7 à droite des numérateurs.
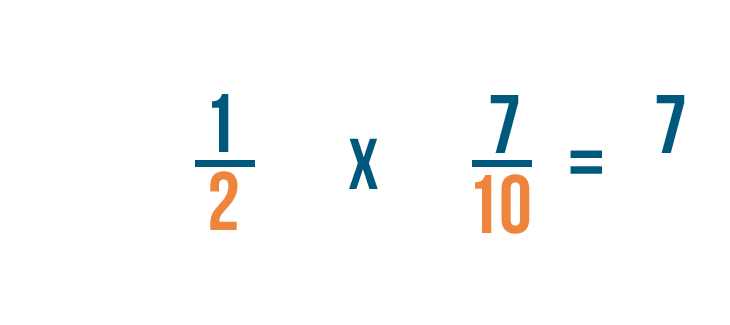
Lorsque nous avons additionné des fractions, les dénominateurs sont restés les mêmes. Mais quand on multiplie, les dénominateurs se multiplient aussi.
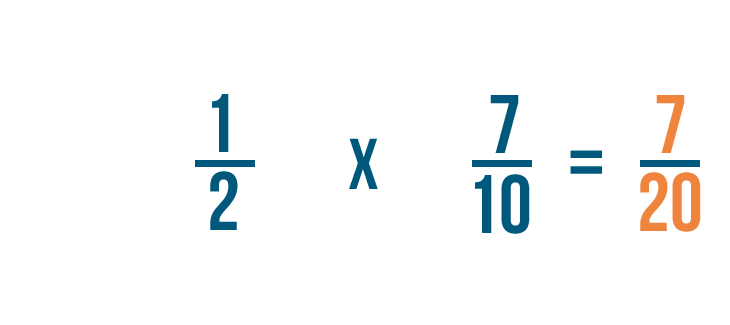
Nous savons maintenant que 1/2 fois 7/10 est égal à 7/20.
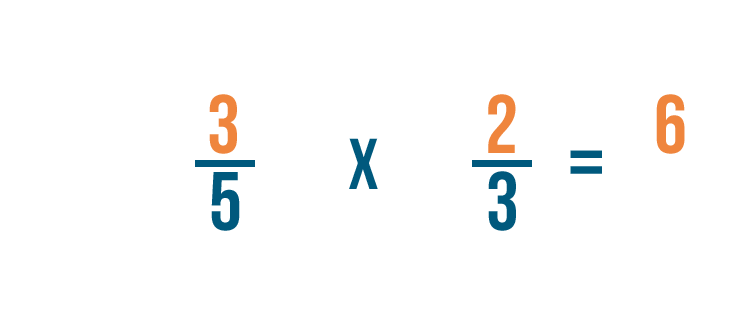
D’abord, nous allons multiplier nos numérateurs. 3 fois 2 égale 6.
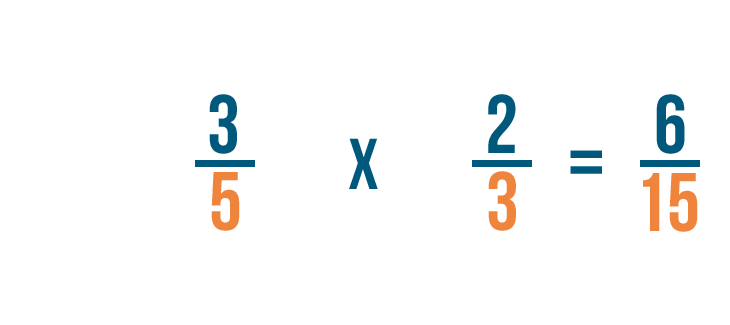
Puis, nous allons multiplier nos dénominateurs. 5 fois 3 est égal à 15.
Essayez !
Essayez de résoudre les problèmes de multiplication ci-dessous.
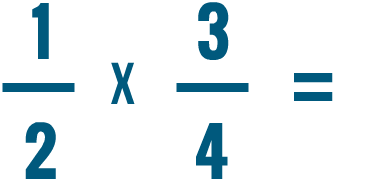
.
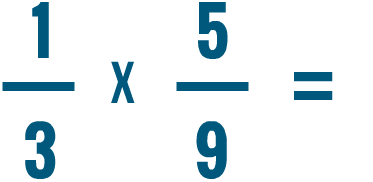
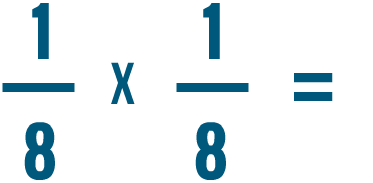
Multiplier une fraction et un nombre entier
Multiplier une fraction et un nombre entier est similaire à la multiplication de deux fractions. Il y a juste une étape supplémentaire : Avant de pouvoir multiplier, vous devrez transformer le nombre entier en fraction. Ce diaporama vous montre comment faire.
Cliquez sur le diaporama pour apprendre à multiplier une fraction et un nombre entier.
-
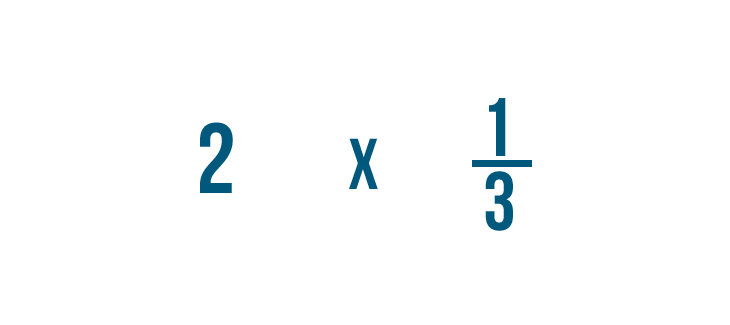
Multiplions 2 fois 1/3. N’oubliez pas que c’est juste une autre façon de demander : » Quel est le 1/3 de 2 ? «
-
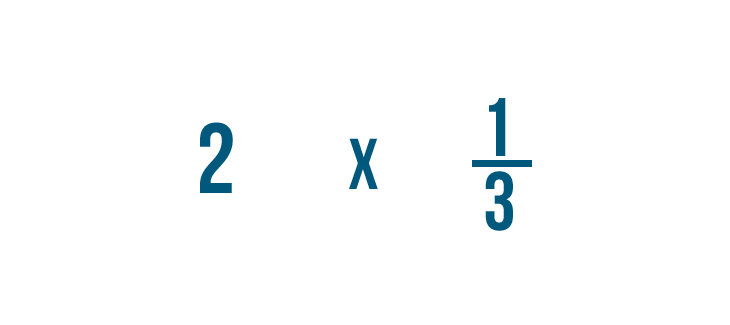
Avant de commencer, nous devons nous assurer que ces nombres sont prêts à être multipliés.
-
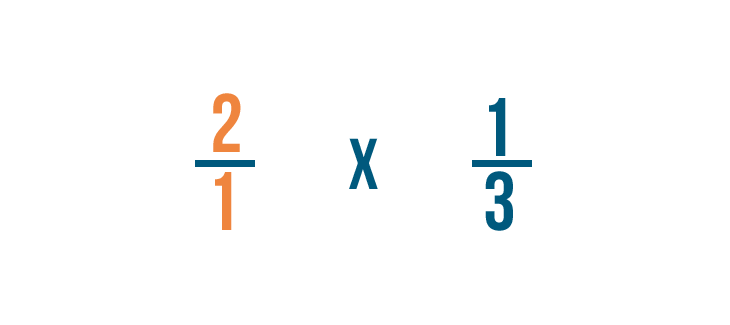
Comme vous l’avez appris dans Introduction aux fractions, nous pouvons aussi écrire 2 sous la forme 2/1.C’est parce que 2 peut être divisé par 1 deux fois.
-
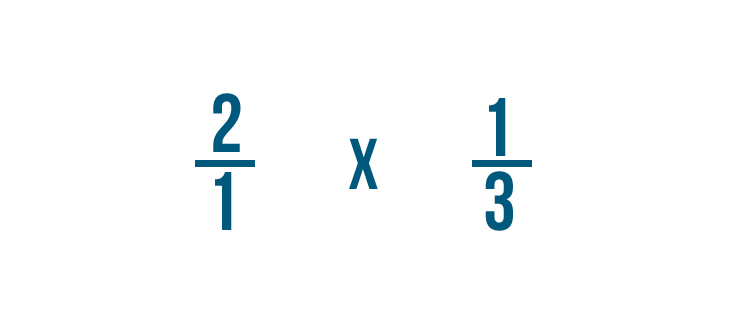
Maintenant nous sommes prêts à multiplier !
-
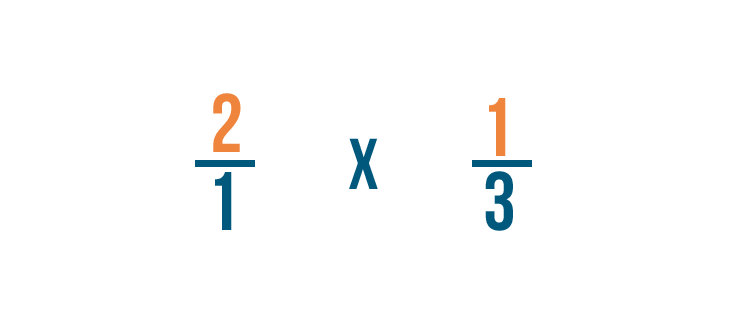
D’abord, nous allons multiplier les numérateurs : 2 et 1.
-
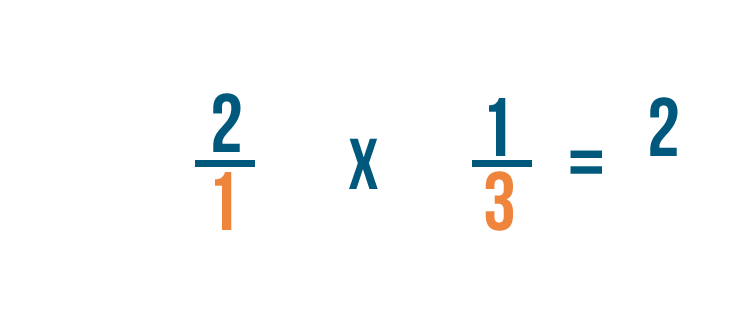
Après, on va multiplier les dénominateurs : 1 et 3.
-
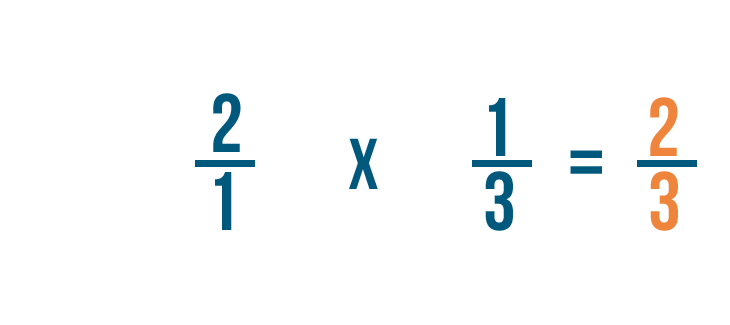
Donc 2/1 fois 1/3 égale 2/3. On pourrait aussi dire que 1/3 de 2 est égal à 2/3.
-
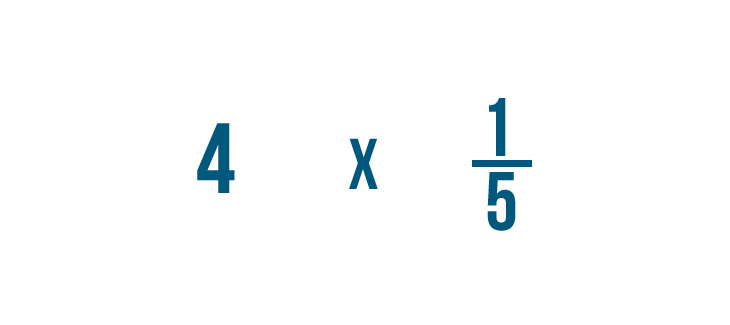
Tentons un autre exemple : 4 fois 1/5.
-
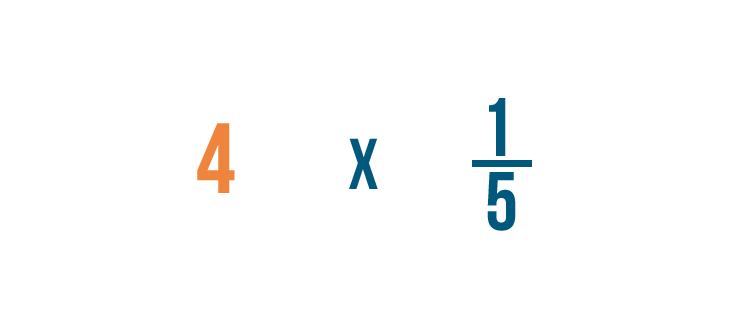
Nous allons devoir écrire 4 sous forme de fraction avant de commencer.
-
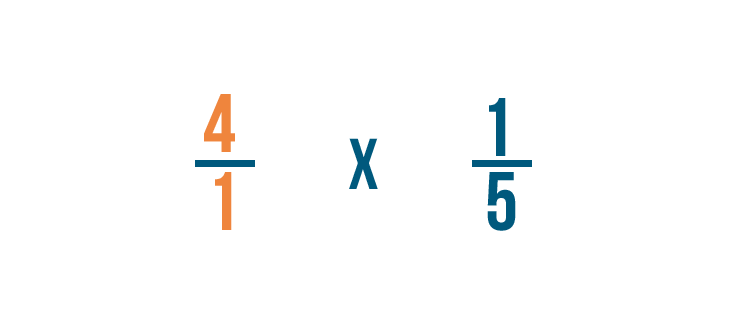
Nous allons écrire 4 sous forme de 4/1. Maintenant, nous sommes prêts à multiplier.
-
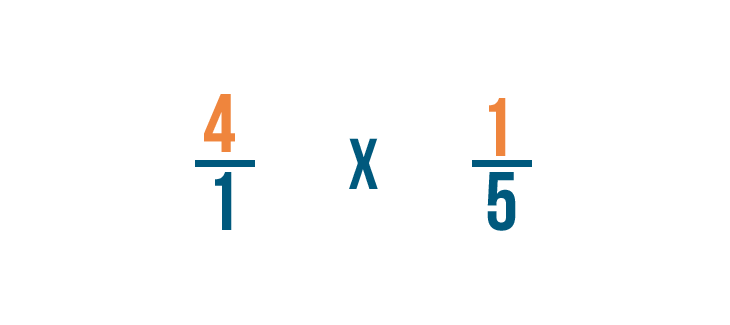
D’abord, nous allons multiplier les numérateurs : 4 et 1.
-
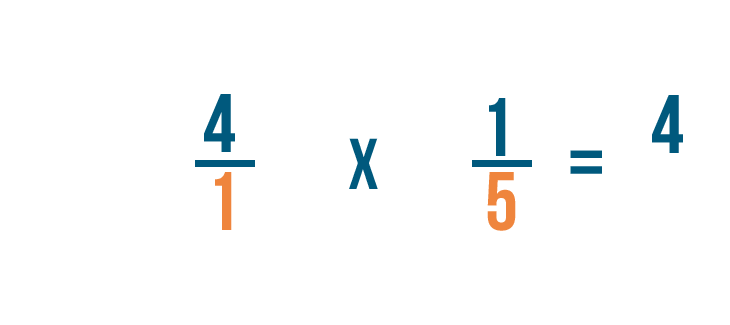
Puis, nous allons multiplier les dénominateurs : 1 et 5.
-
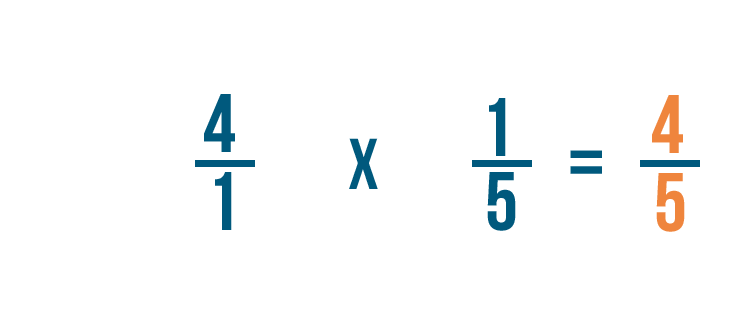
Donc 4/1 fois 1/5 égale 4/5.

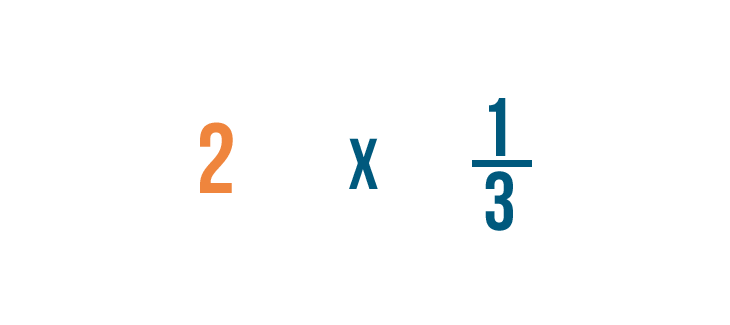
Nous ne pouvons pas multiplier un nombre entier et une fraction, nous allons donc devoir écrire 2 sous forme de fraction.
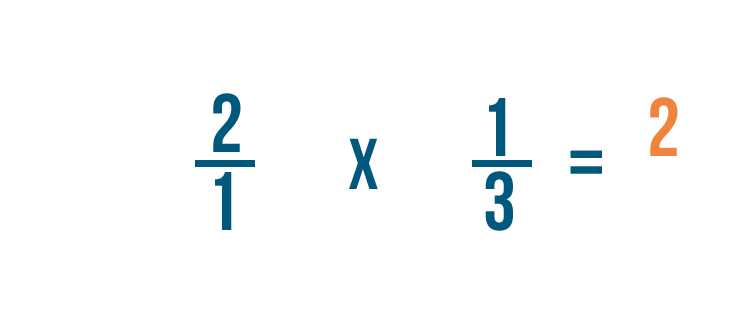
2 fois 1 égale 2. On va aligner le 2 avec les numérateurs.
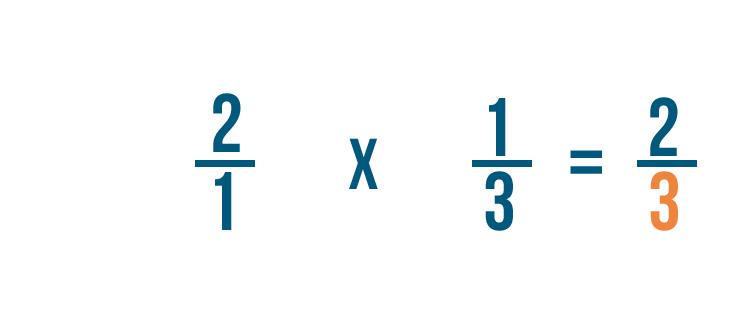
1 fois 3 égale 3. Nous allons aligner le 3 avec les dénominateurs.
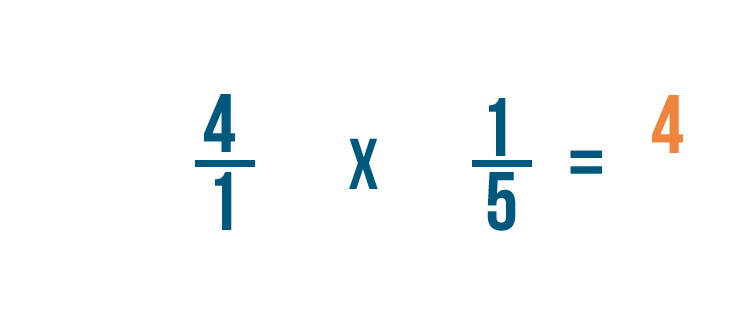
4 fois 1 égale 4, donc le numérateur de notre réponse est 4.
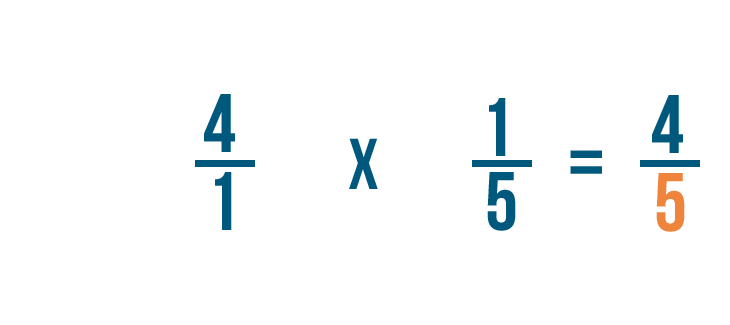
1 fois 5 égale 5, donc 5 est le dénominateur de notre réponse.
Essayez ça!
Essayez de résoudre les problèmes de multiplication ci-dessous.
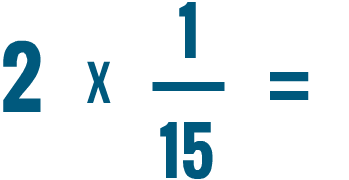
.
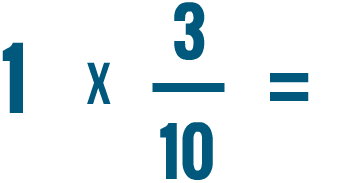
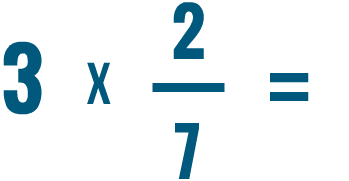
Diviser des fractions
Au cours des dernières pages, vous avez appris à multiplier des fractions. Vous avez peut-être deviné que vous pouvez aussi diviser des fractions. Vous divisez des fractions pour voir combien de parties de quelque chose sont dans quelque chose d’autre. Par exemple, si vous voulez savoir combien de quarts de pouce sont dans quatre pouces, vous pouvez diviser 4 par 1/4.
Tentons un autre exemple. Imaginez qu’une recette demande 3 tasses de farine, mais que votre tasse à mesurer ne contient que 1/3, ou un tiers, de tasse. Combien de tiers de tasse devez-vous ajouter ?
Nous devrons trouver combien de tiers de tasse il y a dans trois tasses. En d’autres termes, nous devrons diviser trois par un tiers.
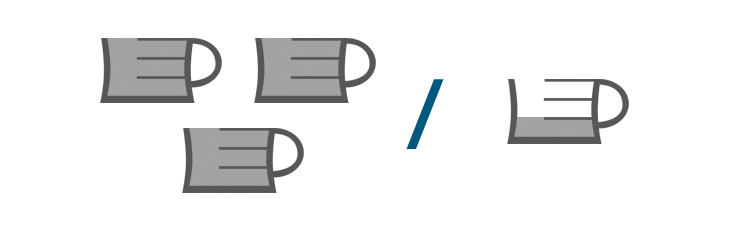
Nous écririons le problème comme ceci :
3 ÷ 1/3
Essayez !
Essayez de poser ces problèmes de division avec des fractions. Ne vous inquiétez pas encore de les résoudre !
Une recette demande 3/4 de tasse d’eau. Vous n’avez qu’une tasse à mesurer de 1/8.

Résoudre des problèmes de division avec des fractions
Maintenant que nous savons comment écrire des problèmes de division, exerçons-nous en résolvant quelques-uns. La division de fractions ressemble beaucoup à la multiplication. Elle nécessite juste une étape supplémentaire. Si vous pouvez multiplier des fractions, vous pouvez aussi les diviser !
Cliquez dans le diaporama pour apprendre à diviser un nombre entier par une fraction.
-
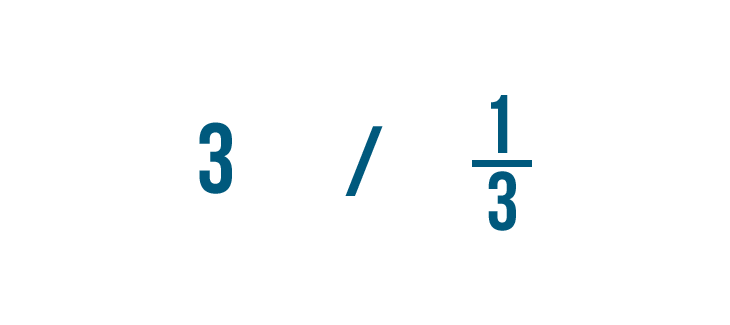
Divisons 3 par 1/3. N’oubliez pas que c’est juste une autre façon de demander : » Combien de tiers y a-t-il dans 3 ? «
-
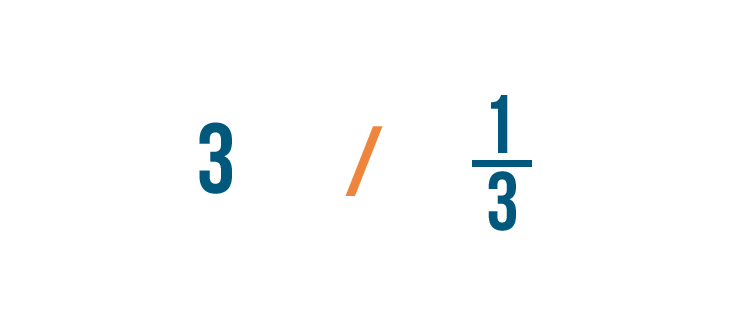
Dans notre leçon sur la division, vous avez appris à écrire le signe de division comme ceci (/).
-
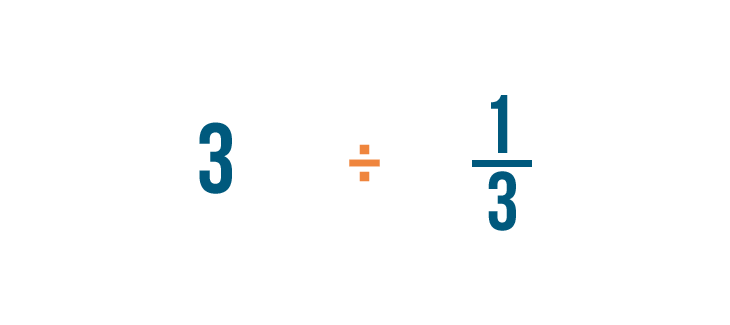
Lorsqu’on divise des fractions, il sera utile d’utiliser l’autre symbole de la division (÷) pour ne pas la confondre avec une fraction.
-
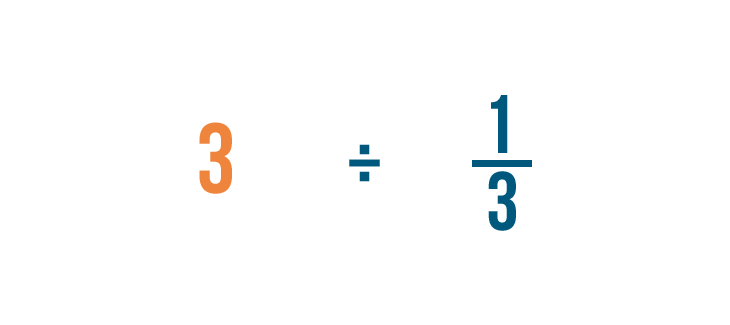
Comme pour la multiplication, nous allons commencer par chercher tous les nombres entiers dans notre problème. Il y en a un : 3.
-
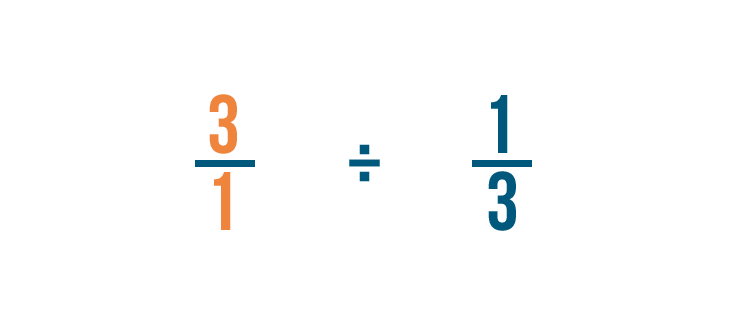
Souvenez-vous que 3 est la même chose que 3/1.
-
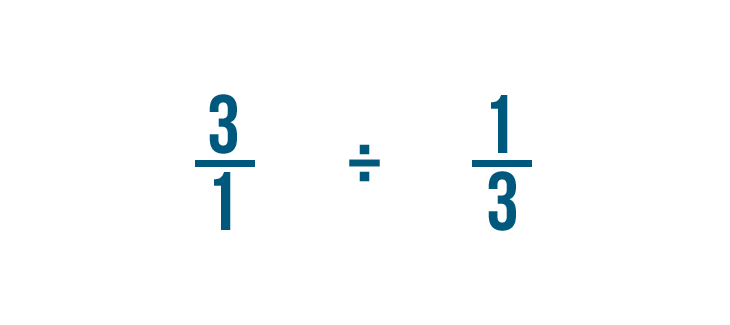
Avant de pouvoir diviser, nous devons effectuer un autre changement.
-
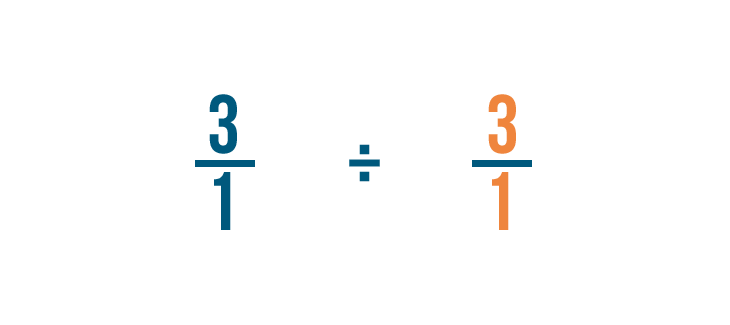
Donc 1/3 devient 3/1.
-
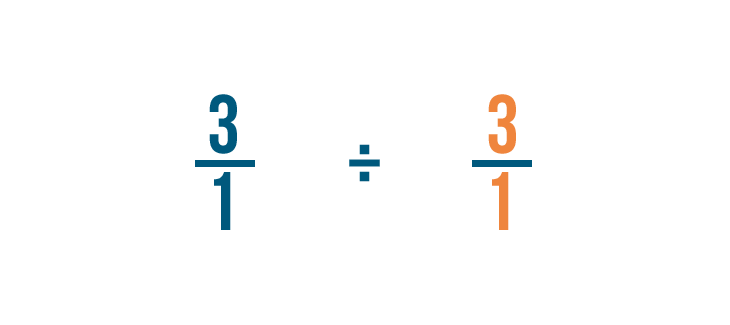
C’est ce qu’on appelle trouver la réciproque, ou l’inverse multiplicatif, de la fraction.
-
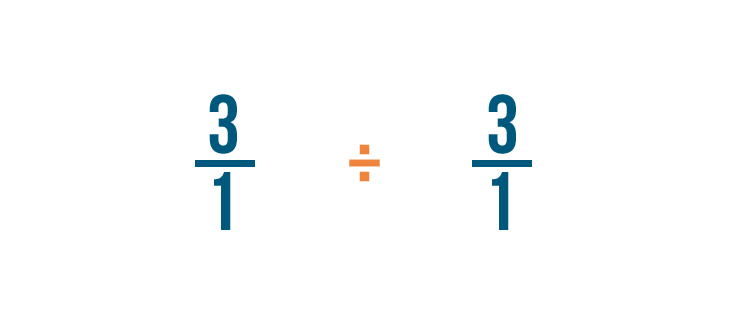
Puisque nous échangeons notre fraction d’origine, nous allons également échanger le signe de division (÷) contre un signe de multiplication (x).
-
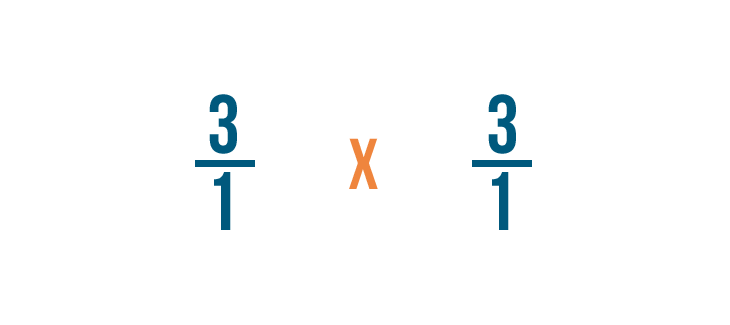
C’est parce que la multiplication est l’inverse de la division.
-
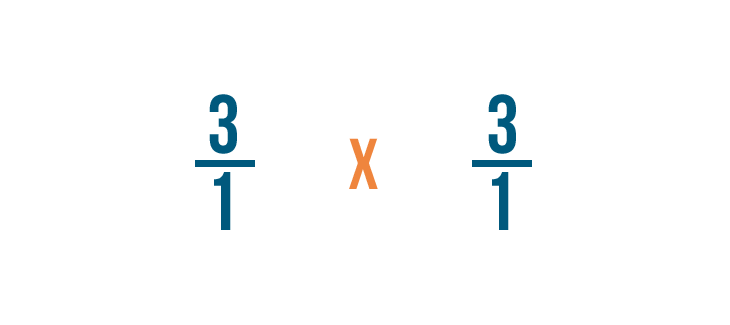
Nous pouvons maintenant traiter ce problème comme un problème de multiplication ordinaire.
-
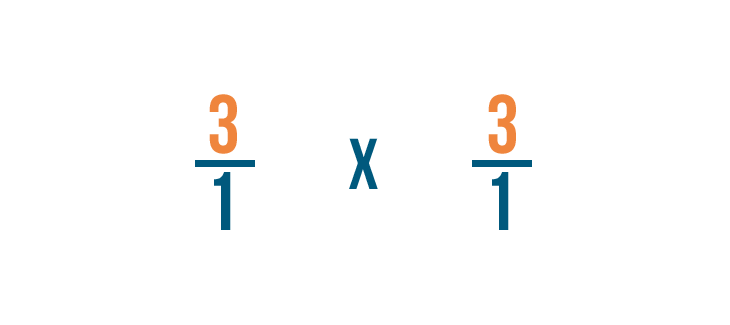
D’abord, nous allons multiplier les numérateurs : 3 et 3.
-
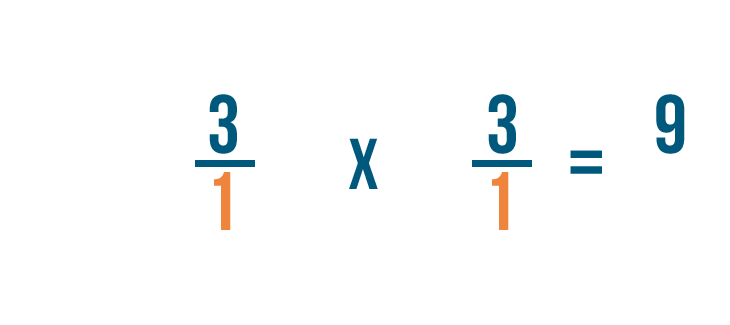
Puis, nous allons multiplier les dénominateurs : 1 et 1.
-
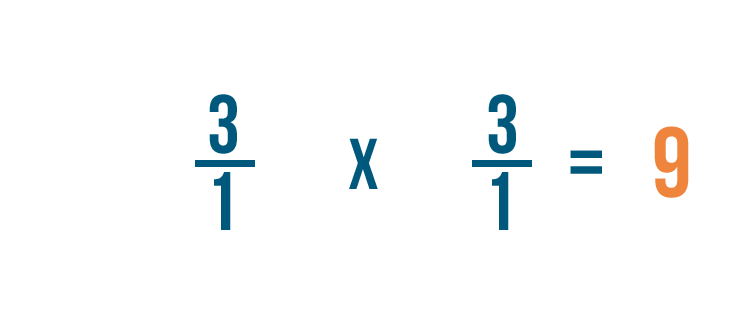
Rappellez-vous que toute fraction supérieure à 1 peut aussi être exprimée sous forme de nombre entier. Ainsi, 9/1 = 9.
-
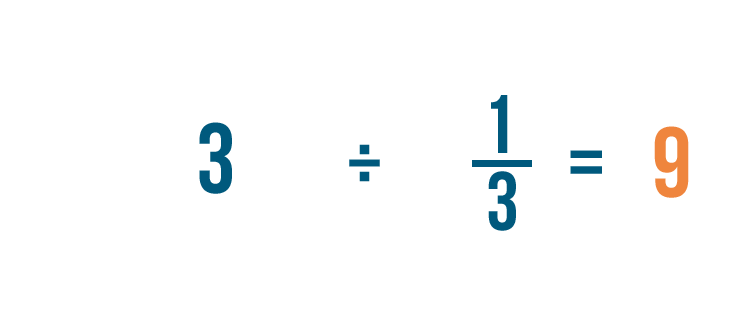
3 ÷ 1/3 = 9. Autrement dit, il y a 9 tiers dans 3.
-
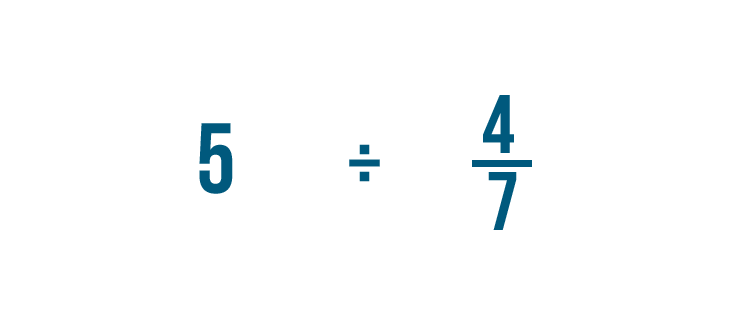
Tentons un autre exemple : 5 divisé par 4/7.
-
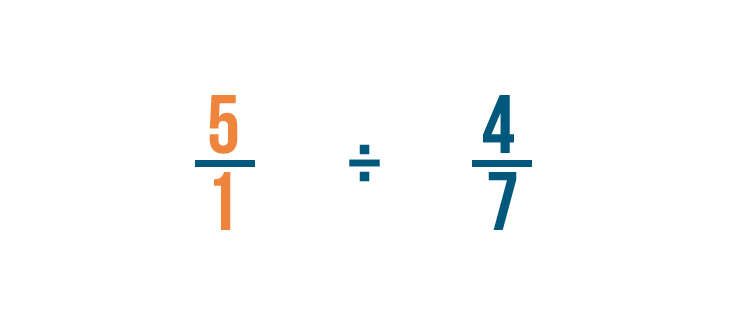
Comme toujours, nous allons réécrire tous les nombres entiers, ainsi 5 devient 5/1.
-
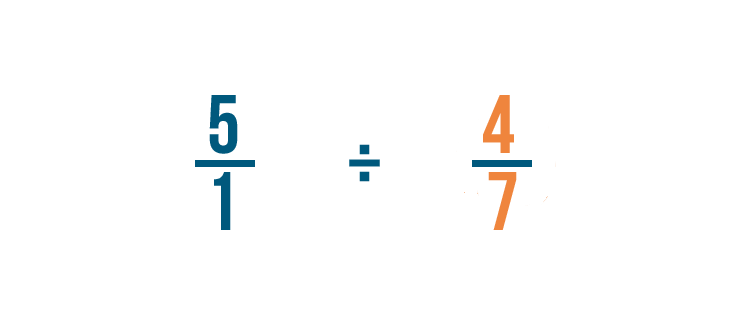
Puis, nous allons trouver la réciproque de 4/7. C’est la fraction par laquelle nous allons diviser.
-
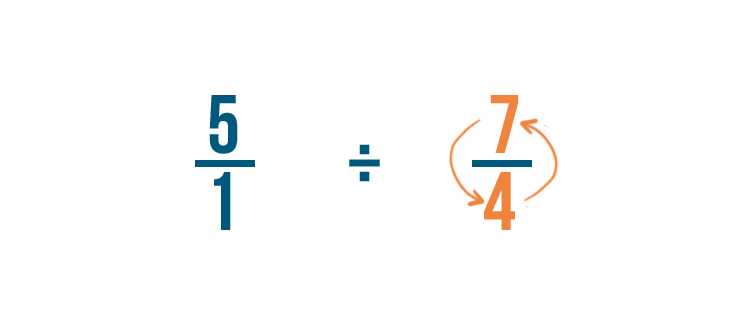
Pour cela, nous allons intervertir le numérateur et le dénominateur, ainsi 4/7 devient 7/4.
-
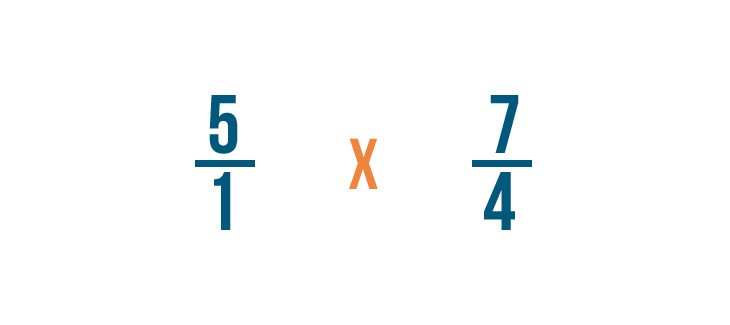
Puis nous allons changer le signe de division (÷) en signe de multiplication (x).
-
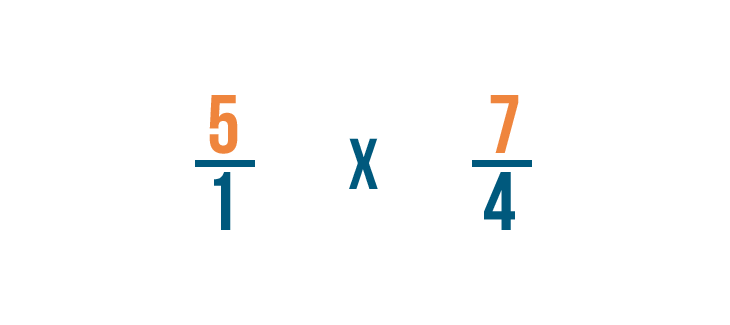
Maintenant nous pouvons multiplier comme nous le ferions normalement. D’abord, nous allons multiplier les numérateurs : 5 et 7.
-
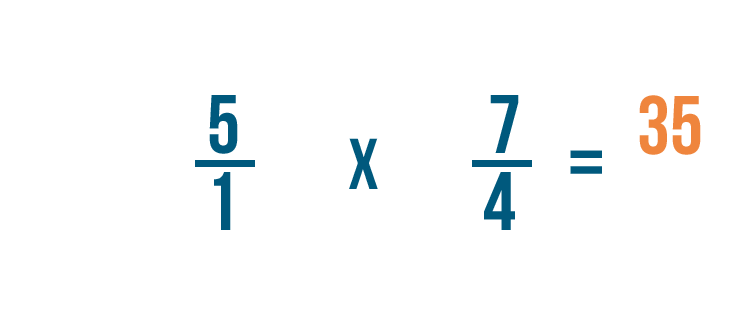
5 fois 7 égale 35, nous allons donc écrire cela à côté des numérateurs.
-
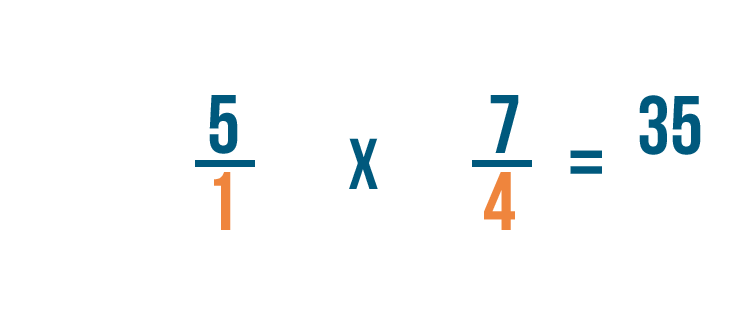
Puis, nous allons multiplier les dénominateurs : 1 et 4.
-
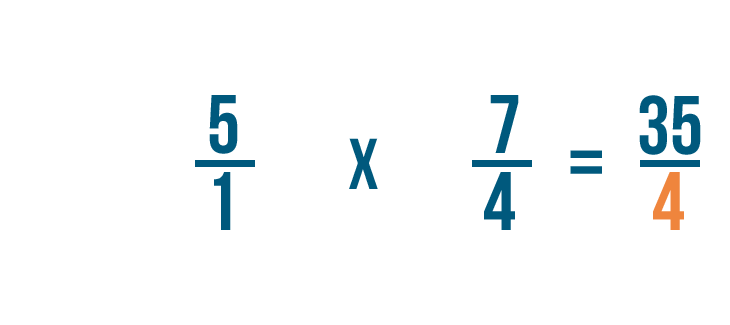
1 fois 4 égale 4, nous allons donc écrire cela à côté des dénominateurs.
-
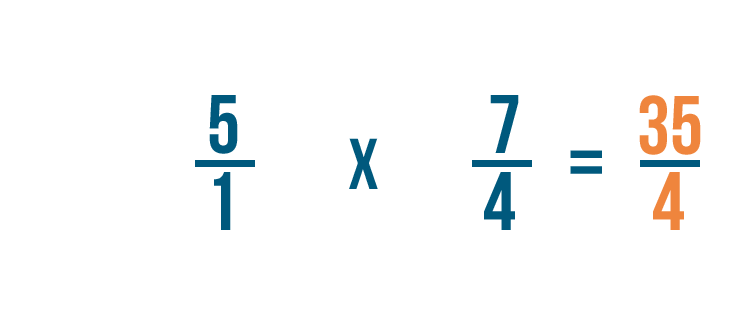
Donc 5/1 x 4/7 = 35/4.
-
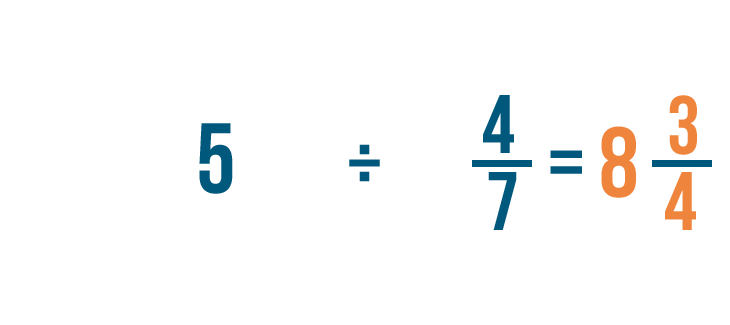
35/4 = 8 3/4. Donc 5 ÷ 4/7 = 8 3/4.

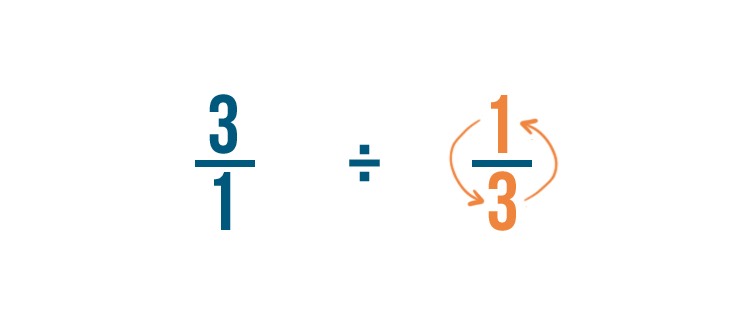
Nous allons intervertir le numérateur et le dénominateur de la fraction par laquelle nous divisons : 1/3 dans cet exemple.
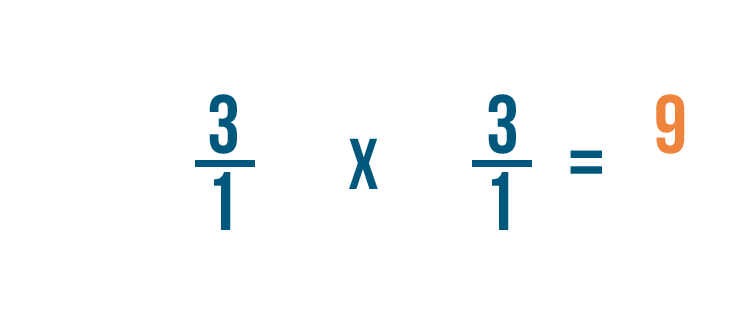
3 fois 3 égale 9, nous allons donc écrire cela à côté des numérateurs.
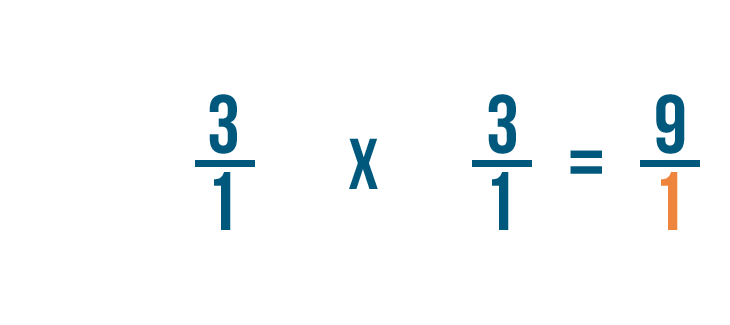
1 fois 1 égale 1, nous allons donc écrire 1 à côté du dénominateur.
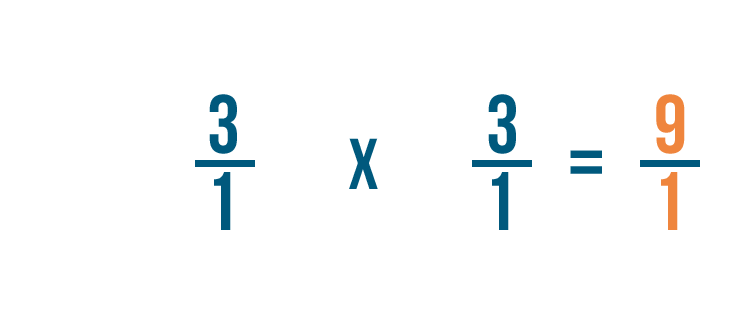
Comme vous pouvez le constater, 3/1 x 1/3 = 9/1.
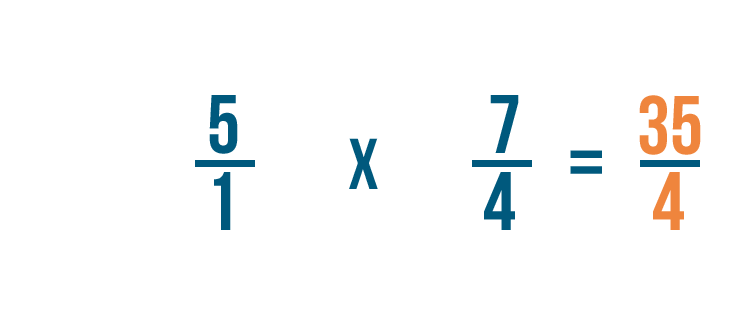
Comme vous l’avez appris précédemment, nous pourrions convertir notre fraction impropre en un nombre mixte pour rendre notre réponse plus facile à lire.
Essayez ça!
Essayez de résoudre ces problèmes de division. Ne vous inquiétez pas de la réduction de la réponse pour le moment.
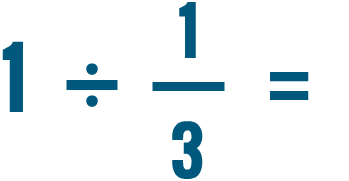
.
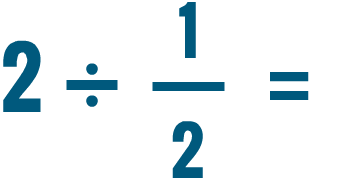
.
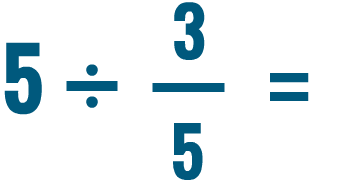
Division de deux fractions
Nous venons d’apprendre à diviser un nombre entier par une fraction. Vous pouvez utiliser la même méthode pour diviser deux fractions.
Cliquez dans le diaporama pour apprendre à diviser avec deux fractions.
-
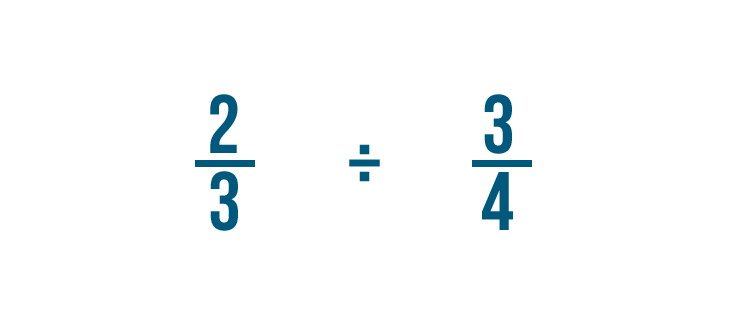
Tentons un problème avec deux fractions : 2/3 ÷ 3/4. Ici, nous voulons savoir combien de 3/4 sont dans 2/3.
-
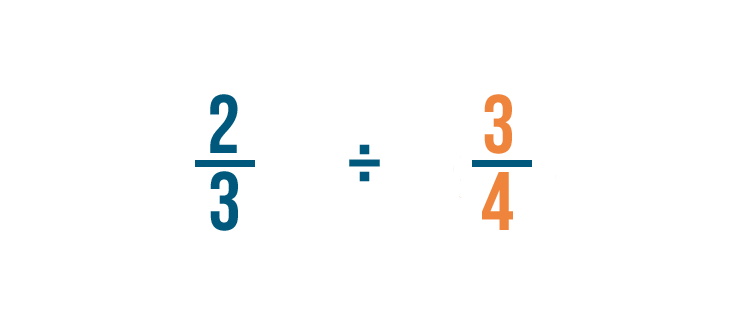
D’abord, nous allons trouver l’inverse de la fraction par laquelle nous divisons : 3/4.
-
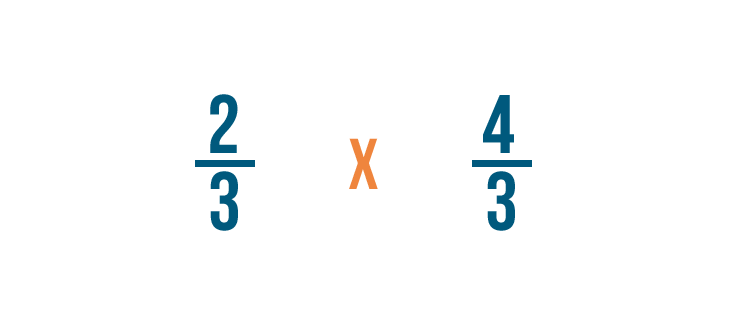
Puis, nous allons changer le signe de division (÷) en signe de multiplication (x).
-
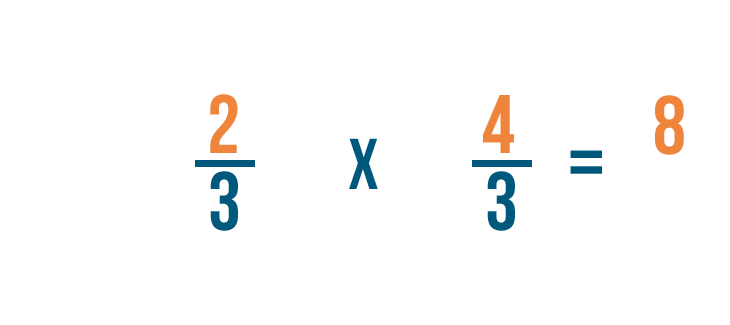
Nous allons maintenant multiplier les numérateurs. 2 x 4 = 8, nous allons donc écrire 8 à côté des chiffres du haut.
-
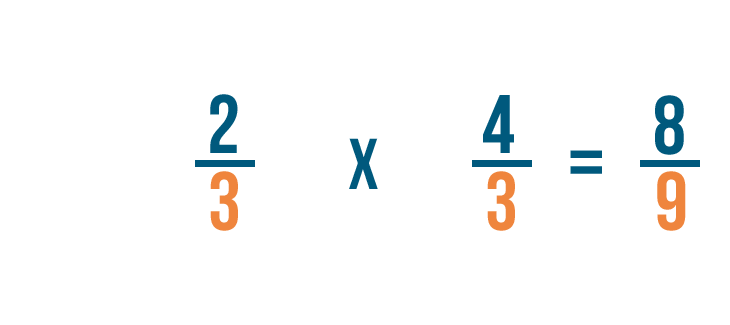
Puis, nous allons multiplier les dénominateurs. 3 x 3 = 9, nous allons donc écrire 9 à côté des chiffres du bas.
-
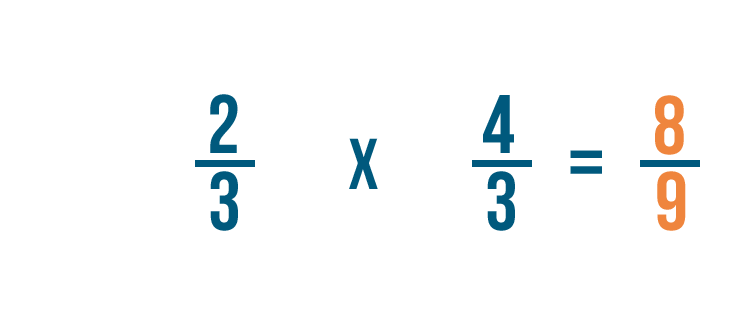
Donc 2/3 x 4/3 = 8/9.
-
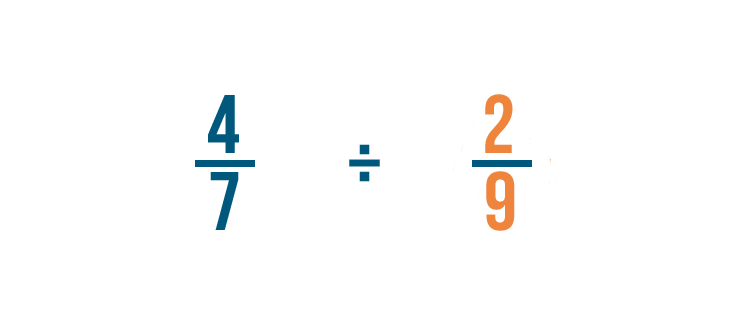
Il n’y a pas de nombre entier, on va donc trouver l’inverse de la fraction par laquelle on divise. C’est 2/9.
-
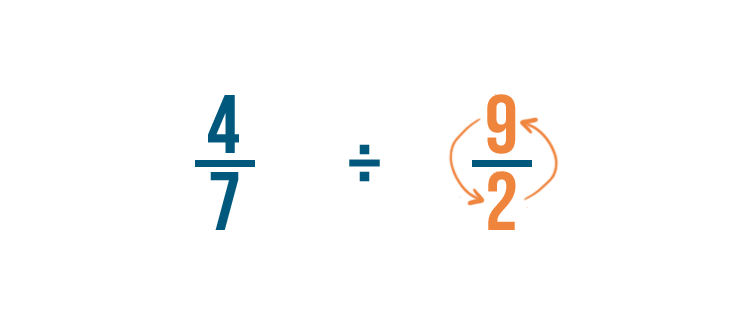
Pour cela, on va intervertir le numérateur et le dénominateur. Ainsi 2/9 devient 9/2.
-
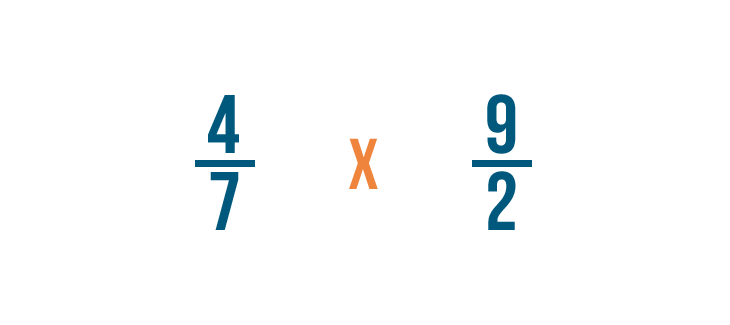
Maintenant, nous allons changer le signe de division (÷) en signe de multiplication (x) et multiplier normalement.
-
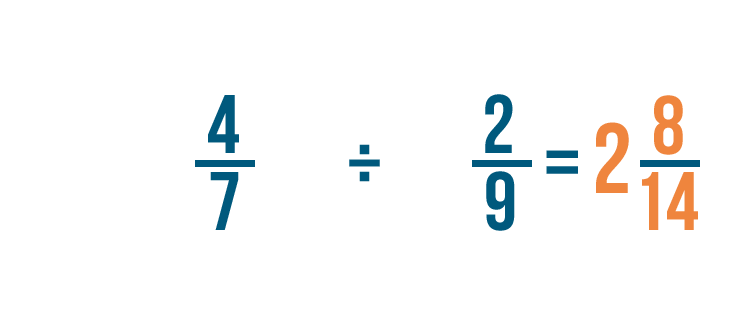
Donc 4/7 ÷ 2/9 = 2 8/14.

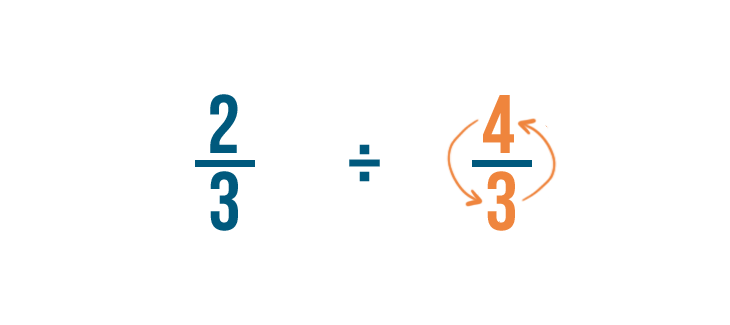
Pour cela, nous allons intervertir le numérateur et le dénominateur. Ainsi 3/4 devient 4/3.
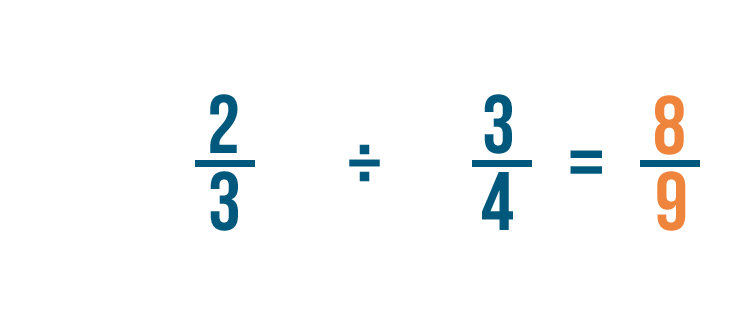
On pourrait aussi écrire cela comme 2/3 ÷ 3/4 = 8/9.
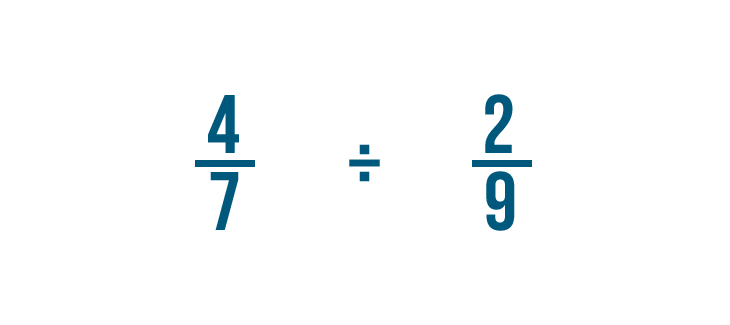
Tentons un autre exemple : 4/7 divisé par 2/9.
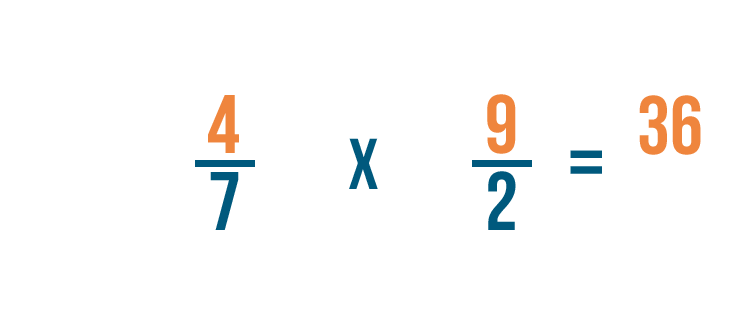
D’abord, nous allons multiplier les numérateurs. 4 x 9 = 36.
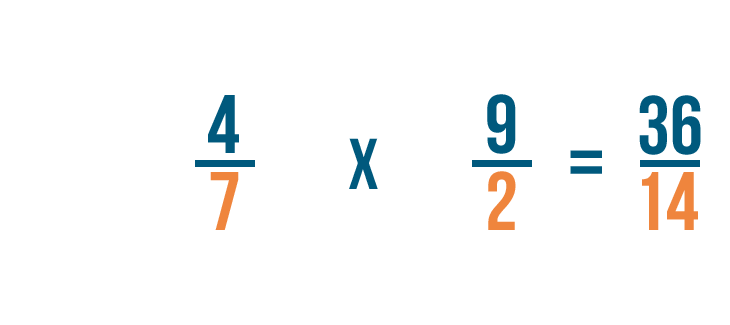
Puis, nous allons multiplier les dénominateurs. 7 x 2 = 14.
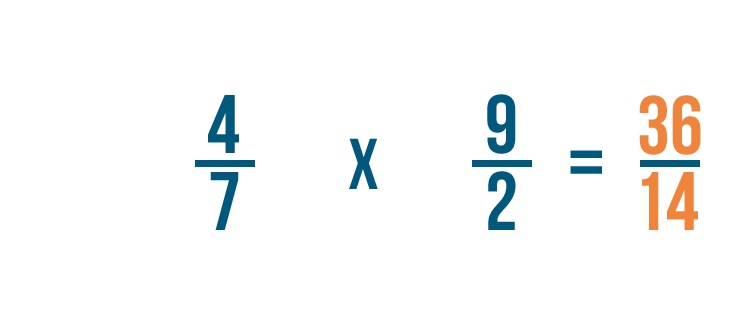
Donc 4/7 x 9/2 = 36/14. Comme précédemment, vous pouvez convertir cette fraction impropre en un nombre mixte.
Essayez ça!
Essayez de résoudre ces problèmes de division. Ne vous inquiétez pas de la réduction de la réponse pour le moment.
.
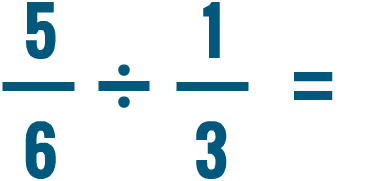
.
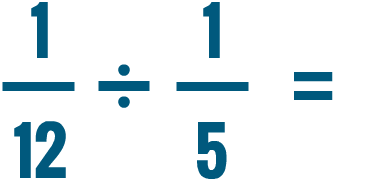
Multiplication et division de nombres mixtes
Comment résoudriez-vous un problème comme celui-ci ?
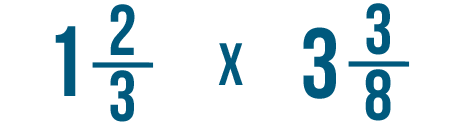
Comme vous l’avez appris dans la leçon précédente, chaque fois que vous résolvez un problème avec un nombre mixte, vous devrez d’abord le convertir en fraction impropre. Ensuite, vous pouvez multiplier ou diviser comme d’habitude.
Utiliser l’annulation pour simplifier les problèmes
Parfois, vous pourriez avoir à résoudre des problèmes comme celui-ci :
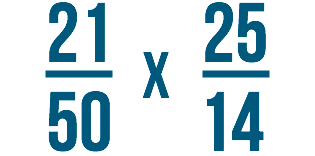
Ces deux fractions comprennent de grands nombres. Vous pourriez multiplier ces fractions de la même manière que toutes les autres fractions. Cependant, les grands nombres comme celui-ci peuvent être difficiles à comprendre. Pouvez-vous imaginer 21/50, ou vingt et un cinquantièmes, dans votre tête ?
21/50 x 25/14 = 525/700
Même la réponse semble compliquée. C’est 525/700, soit cinq cent vingt-cinq sept centièmes. Quelle gueule !
Si vous n’aimez pas travailler avec de grands nombres, vous pouvez simplifier un problème comme celui-ci en utilisant une méthode appelée annulation. Lorsque vous annulez les fractions dans un problème, vous les réduisez toutes les deux en même temps.
L’annulation peut sembler compliquée au début, mais nous allons vous montrer comment la faire étape par étape. Reprenons l’exemple que nous venons de voir.
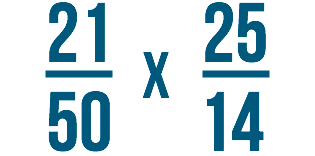
Etape 1
Pour commencer, regardez le numérateur de la première fraction et le dénominateur de la seconde. Nous voulons voir s’ils peuvent être divisés par le même nombre.
Dans notre exemple, il semble que 21 et 14 puissent tous deux être divisés par 7.
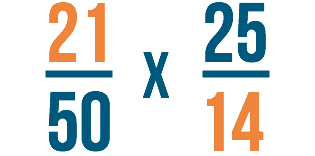
Étape 2
Puis, nous allons diviser 21 et 14 par 7. D’abord, nous allons diviser notre nombre supérieur à gauche : 21.
21 ÷ 7 = 3
Puis nous allons diviser le nombre inférieur à droite : 14.
14 ÷ 7 = 2
Nous écrirons les réponses à chaque problème à côté des nombres que nous avons divisés. Puisque 21 ÷ 7 est égal à 3, nous écrirons 3 à l’endroit où se trouvait le 21. 14 ÷ 7 est égal à 2, nous écrirons donc 2 à la place du 14. Nous pouvons rayer, ou annuler, les nombres avec lesquels nous avons commencé.
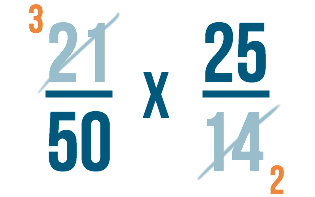
Notre problème semble beaucoup plus simple maintenant, n’est-ce pas ?
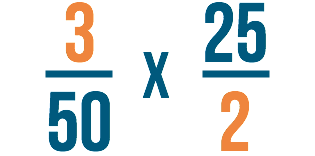
Étape 3
Regardons les autres nombres de la fraction. Cette fois, nous allons regarder le dénominateur de la première fraction et le numérateur de la seconde. Peuvent-ils être divisés par le même nombre ?
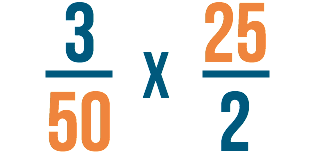
Vous avez remarqué qu’ils peuvent tous deux être divisés par 25 ! Vous avez peut-être aussi remarqué qu’ils peuvent tous deux être divisés par 5. Nous pourrions aussi utiliser 5, mais généralement, lorsque vous annulez, vous voulez chercher le plus grand nombre par lequel les deux nombres peuvent être divisés. De cette façon, vous n’aurez pas à réduire à nouveau la fraction à la fin.
Étape 4
Après, nous allons annuler comme nous l’avons fait à l’étape 2.
Nous allons diviser notre nombre du bas à gauche : 50.
50 ÷ 25 = 2
Puis nous allons diviser le nombre du haut à droite : 25.
25 ÷ 25 = 1
Nous écrirons les réponses à chaque problème à côté des nombres que nous avons divisés.
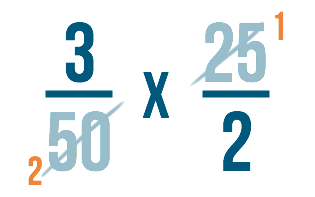
Étape 5
Maintenant que nous avons annulé les fractions originales, nous pouvons multiplier nos nouvelles fractions comme nous le ferions normalement. Comme toujours, multipliez d’abord les numérateurs :
3 x 1 = 3
Puis multipliez les dénominateurs :
2 x 2 = 4
Donc 3/2 x 1/2 =3/4, ou trois quarts.
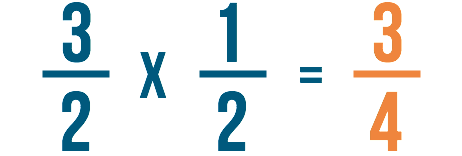
Étape 6
Enfin, vérifions à nouveau notre travail. 525/700 aurait été notre réponse si nous avions résolu le problème sans annuler. Si nous divisons à la fois 525 et 700 par 175, nous pouvons voir que 525/700 est égal à 3/4.
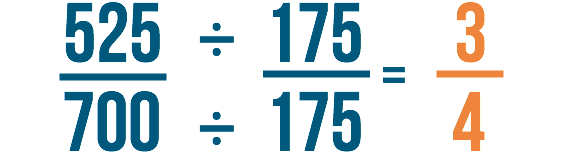
Nous pourrions également dire que nous réduisons 525/700 à 3/4. N’oubliez pas que l’annulation est juste une autre façon de réduire les fractions avant de résoudre un problème. Vous obtiendrez la même réponse, quel que soit le moment où vous les réduisez.
/fr/fractions/conversion-de-pourcentages-décimaux-et-fractions/content/
0 commentaire