=================================================================================
Dans la théorie classique de la diffraction, la diffraction de Bragg se produit lorsque des ondes de particules chargées ou de rayonnement électromagnétique ayant une longueur d’onde comparable à l’espacement atomique sont incidentes sur un échantillon cristallin. Les ondes réfléchies par des centres de diffusion adjacents doivent avoir une différence de trajet égale à un nombre entier de longueurs d’onde. Les ondes diffusées interfèrent de manière constructive si elles restent en phase. Par conséquent, la différence de trajet entre les ondes électroniques réfléchies par les plans supérieur et inférieur de la figure 3882 est égale à la longueur totale (AO+BO). En supposant que les plans hkl sont espacés d’une distance dhkl et que l’onde est incidente et réfléchie à des angles θB, AB et BC sont tous deux égaux à dsin(θB) et la différence de trajet totale devrait être égale à 2dsin(θB).
Comme discuté à la page2678, on peut avoir,
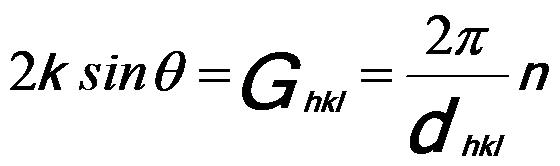 ——————————————
——————————————
où,
n — Le multiple entier du plus petit Ghkl qui est autorisé,
k = 2π/λ.
On peut donc obtenir la condition de diffraction de Bragg bien connue, donnée par,
nλ = 2dhklsin(θB) ——————————————–
où,
n — Un nombre entier, l’ordre de réflexion;
dhkl — L’espacement de réseau de (hkl) ;
λ — La longueur d’onde de la particule chargée ou des ondes de rayonnement électromagnétique;
θB — L’angle de Bragg qui est l’angle entre le vecteur d’onde incidente et les plans du réseau comme indiqué sur la figure 3882,
hkl — Les indices de Miller.
L’angle de Bragg θB est un concept très important dans la théorie de la diffraction, par exemple, largement utilisé pour expliquer les phénomènes de diffraction des électrons et des rayons X. De très fortes intensités connues sous le nom de pics de Bragg sont obtenues dans le schéma de diffraction lorsque les ondes diffusées satisfont à la condition de Bragg. L’angle entre les ondes incidentes et réfléchies est égal à 2θB comme le montre la figure 3882.
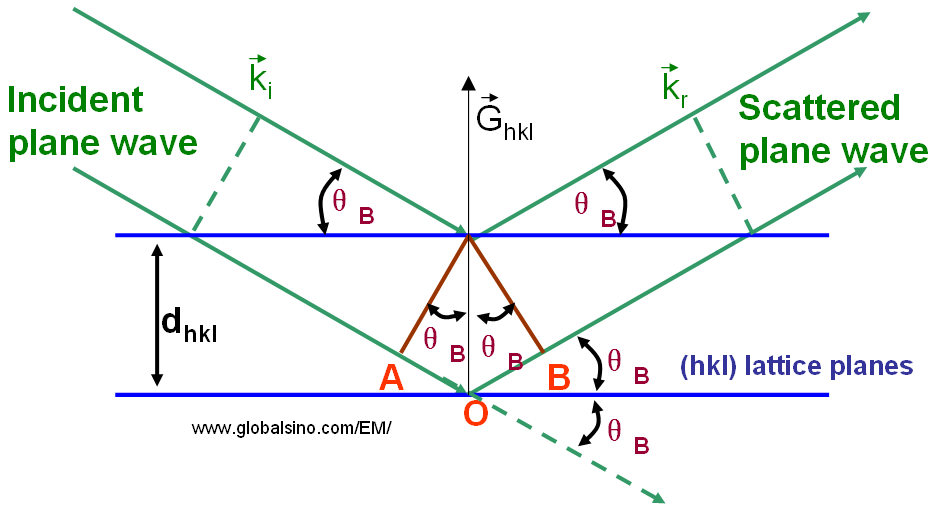
La différence de parcours entre les ondes réfléchies est égale à AO + BO.
Pour les structures FCC et BCC, les constantes de réseau sont données par, (Vous pouvez télécharger le fichier excel pour vos propres calculs)
—————–
Le tableau 3882a montre que les électrons interagissent avec 1 électron, plusieurs électrons, 1 noyau et plusieurs noyaux dans les solides.
| Interaction avec . électron(s) | Interaction avec le noyau/les noyaux | ||||
|---|---|---|---|---|---|
| 1 électron | Plusieurs électrons | 1 noyau | Plusieurs noyaux | Tre> | Type de diffusion | Inelastique | Inelastique | Quasi-élastique | Elastic | Inelastic |
| Effet de diffusion | Effet Compton des électrons ; excitation des électrons (de 50 eV à quelques keV : EDS et EELS) | Excitation plasmonique (< 50 eV, échantillon TEM ~100 nm) ; effet Cerenkov | Diffusion Rutherford ; diffusion de phonons (< 1 eV, chaleur) | Diffusion de Bragg | Bremsstrahlung |
Le tableau 3882b présente quelques exemples d’angles de Bragg à diverses tensions de faisceau pour un espacement d typique. Les angles de Bragg ont été obtenus avec l’équation 3882b (pour n = 1).
Tableau 3882b. Angles de Bragg à différentes tensions de faisceau pour un espacement d typique.
| Voltage d’accélération (kV) | Longueur d’onde (nm) | Cristaux | d-(nm) | Angle de Bragg (° & mrad) |
| 100 | 0.0037 | Cristaux biologiques typiques | 10 | 0,0106° (0,19 mrad) | 200 | 0,0025 | Nickel (Ni) | 0,203 | 0.353° (6,16 mrad) |
Dans les expériences réelles, différentes de la diffusion diffuse, les pics de Bragg proviennent de la structure ordonnée à longue portée. Les spécimens cristallins doivent être inclinés dans un goniomètre en TEM afin de :
i) Observer les franges du réseau et les structures cristallines.
ii) Déterminer l’orientation du cristal.
iii) Observer le contraste de diffraction des défauts du réseau avec certaines réflexions de Bragg ou une orientation connue.
iv) Déterminer le vecteur de Burgers des défauts du réseau.
Tableau 3882c. Scripts de micrographie numérique pour calculer les angles de réflexion des cristaux.
| Structure cristalline | Scripts |
| FCC | Diffraction des électrons, XRD | BCC | Diffraction des électrons, XRD |
.
0 commentaire