Parfois, il y a plus d’une façon de résoudre un problème. Nous devons apprendre à comparer les performances de différents algorithmes et à choisir le meilleur pour résoudre un problème particulier. Lors de l’analyse d’un algorithme, nous considérons principalement la complexité temporelle et la complexité spatiale. La complexité temporelle d’un algorithme quantifie le temps d’exécution d’un algorithme en fonction de la longueur de l’entrée. De même, la complexité spatiale d’un algorithme quantifie la quantité d’espace ou de mémoire prise par un algorithme pour s’exécuter en fonction de la longueur de l’entrée.
La complexité temporelle et spatiale dépend de beaucoup de choses comme le matériel, le système d’exploitation, les processeurs, etc. Cependant, nous ne considérons aucun de ces facteurs lors de l’analyse de l’algorithme. Nous ne considérerons que le temps d’exécution d’un algorithme.
Débutons par un exemple simple. Supposons que l’on vous donne un tableau $A$ et un entier $x$ et que vous devez trouver si $x$ existe dans le tableau $A$.
La solution simple à ce problème est de parcourir tout le tableau $A$ et de vérifier si l’un des éléments est égal à $x$.
for i : 1 to length of A if A is equal to x return TRUEreturn FALSEChacune des opérations de l’ordinateur prend un temps approximativement constant. Soit chaque opération prend $c$$ de temps. Le nombre de lignes de code exécutées dépend en fait de la valeur de $x$. Lors de l’analyse de l’algorithme, nous considérerons le plus souvent le pire scénario, c’est-à-dire lorsque $x$ n’est pas présent dans le tableau $A$. Dans le pire des cas, la condition if sera exécutée $N$$ fois où $N$ est la longueur du tableau $A$. Ainsi, dans le pire des cas, le temps d’exécution total sera $(N * c + c)$. $N * c$ pour la condition if et $c$ pour l’instruction return ( en ignorant certaines opérations comme l’affectation de $i$ ).
Comme on peut le voir, le temps total dépend de la longueur du tableau $A$. Si la longueur du tableau va augmenter, le temps d’exécution va également augmenter.
L’ordre de croissance est la façon dont le temps d’exécution dépend de la longueur de l’entrée. Dans l’exemple ci-dessus, nous pouvons clairement voir que le temps d’exécution dépend linéairement de la longueur du tableau. L’ordre de croissance nous aidera à calculer le temps d’exécution avec facilité. Nous ignorerons les termes d’ordre inférieur, car ils sont relativement insignifiants pour une grande entrée. Nous utilisons une notation différente pour décrire le comportement limite d’une fonction.
Notation $$O$:
Pour désigner la limite supérieure asymptotique, nous utilisons la notation $O$. Pour une fonction donnée $g(n)$, on désigne par $O(g(n))$ (prononcé « big-oh de g de n ») l’ensemble des fonctions :
$O(g(n)) =$ { $f(n)$ : il existe des constantes positives $c$ et $n_0$ telles que $0 \le f (n) \le c * g(n)$ pour tous les $n \ge n_0$ }
$\Omega$-notation:
Pour désigner la borne inférieure asymptotique, on utilise la $\Omega$-notation. Pour une fonction donnée $g(n)$, on désigne par $\Omega(g(n))$ (prononcé « big-omega de g de n ») l’ensemble des fonctions :
$\Omega(g(n)) =$ { $f(n)$ : il existe des constantes positives $c$ et $n_0$ telles que $0 \le c * g(n) \le f(n)$ pour tout $n \ge n_0$ }
$\Theta$-notation:
Pour désigner la borne serrée asymptotique, on utilise la $\Theta$-notation. Pour une fonction donnée $g(n)$, on désigne par $\Theta(g(n))$ (prononcé « big-theta de g de n ») l’ensemble des fonctions :
$\Theta(g(n)) =$ { $f (n)$ : il existe des constantes positives $c_1,\ ;c_2$ et $n_0$ telles que $0 \le c_1 * g(n) \le f (n) \le c_2 * g(n)$ pour tout $n \gt n_0$ }
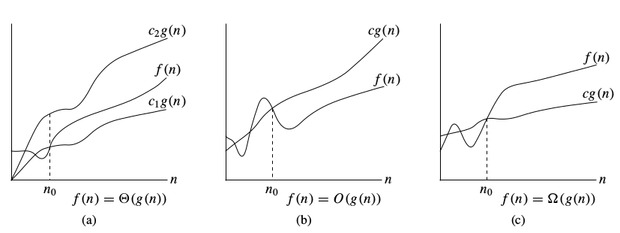
Notations de complexité temporelle
Lorsqu’on analyse un algorithme, nous considérons le plus souvent la notation $O$ car elle nous donnera une limite supérieure du temps d’exécution, c’est-à-dire le temps d’exécution dans le pire des cas.C’est-à-dire le temps d’exécution dans le pire des cas.
Pour calculer $O$-notation, nous allons ignorer les termes d’ordre inférieur, car ceux-ci sont relativement insignifiants pour une grande entrée.
Let $f(N) = 2 * N^2 + 3 * N + 5$
$O(f(N)) = O(2 * N^2 + 3 * N + 5) = O(N^2)$
Voyons quelques exemples:
int count = 0;for (int i = 0; i < N; i++) for (int j = 0; j < i; j++) count++;Voyons combien de fois count++ s’exécutera.
Quand $i = 0$, il s’exécutera $0$$ fois.
Quand $i = 1$, il s’exécutera $1$$ fois.
Quand $i = 2$, il s’exécutera $2$$ fois et ainsi de suite.
Le nombre total de fois où count++ s’exécutera est $0 + 1 + 2 + …. + (N-1) = \frac{N * (N-1)}{2}$. Donc la complexité temporelle sera $O(N^2)$.
int count = 0;for (int i = N; i > 0; i /= 2) for (int j = 0; j < i; j++) count++;C’est un cas délicat. A première vue, il semble que la complexité soit $O(N * logN)$. $N$ pour la boucle $j’s$ et $logN$ pour la boucle $i’s$. Mais c’est faux. Voyons pourquoi.
Pensez au nombre de fois que count++ s’exécutera.
Lorsque $i = N$, il s’exécutera $N$$ fois.
Lorsque $i = N / 2$, il s’exécutera $N / 2$$ fois.
Quand $i = N / 4$, il s’exécutera $N / 4$ fois et ainsi de suite.
Le nombre total de fois que count++ s’exécutera est $N + N / 2 + N / 4 + …. + 1 = 2 * N$. Donc la complexité temporelle sera $O(N)$.
Le tableau ci-dessous a pour but de vous aider à comprendre la croissance de plusieurs complexités temporelles courantes, et ainsi vous aider à juger si votre algorithme est assez rapide pour obtenir un Accepté ( en supposant que l’algorithme est correct ).
| Longueur de l’entrée (N) | La plus mauvaise acceptée. Algorithme | ||
|---|---|---|---|
| $\le $ | $O(N !), O(N^6)$ | ||
| $\le $ | $O(2^N * N^2)$ | ||
| $\le $ | $O(2^N * N)$ | $\le 100$ | $O(N^4)$ | $\le 400$ | $O(N^3)$. |
| 2K$ | O(N^2 * logN)$ | ||
| 1M$ | O(N * logN)$ | ||
| O(N), O(logN), O(1)$ |
Voir le prochain tutoriel
0 commentaire