En statistiques, l’étendue est la propagation de vos données de la valeur la plus basse à la valeur la plus élevée de la distribution. C’est une mesure de variabilité couramment utilisée.
Avec les mesures de tendance centrale, les mesures de variabilité vous donnent des statistiques descriptives pour résumer votre ensemble de données.
L’étendue est calculée en soustrayant la valeur la plus faible de la valeur la plus élevée. Alors qu’un grand intervalle signifie une variabilité élevée, un petit intervalle signifie une faible variabilité dans une distribution.
Table des matières
Calculer l’étendue
La formule pour calculer l’étendue est :
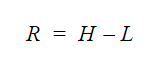
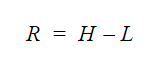
- . R = étendue
- H = valeur la plus élevée
- L = valeur la plus faible
L’étendue est la mesure de variabilité la plus facile à calculer. Pour trouver l’étendue, suivez les étapes suivantes :
- Ordre toutes les valeurs de votre ensemble de données de la plus faible à la plus élevée.
- Soustraire la valeur la plus faible de la valeur la plus élevée.
Ce processus est le même, que vos valeurs soient positives ou négatives, ou qu’il s’agisse de nombres entiers ou de fractions.
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Age | 37 | 19 | 31 | 29 | 21 | 26 | 33 | 36 |
Premièrement, ordonner les valeurs de bas en haut pour identifier la valeur la plus basse (L) et la valeur la plus haute (H).
| Age | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 37 |
|---|
Puis soustraire la valeur la plus faible de la valeur la plus élevée.
R = H – L
R = 37 – 19 = 18
L’étendue de notre ensemble de données est de 18 ans.
À quel point l’étendue est-elle utile ?
L’étendue vous donne généralement un bon indicateur de la variabilité lorsque vous avez une distribution sans valeurs extrêmes. Lorsqu’elle est associée à des mesures de tendance centrale, la plage peut vous renseigner sur l’étendue de la distribution.
Mais la plage peut être trompeuse lorsque vous avez des valeurs aberrantes dans votre ensemble de données. Une valeur extrême dans les données vous donnera une plage complètement différente.
| Age | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 61 |
|---|
En utilisant le même calcul, nous obtenons un résultat très différent cette fois-ci :
R = H – L
R = 61 – 19 = 42
Avec une valeur aberrante, notre fourchette est maintenant de 42 ans.
Dans l’exemple ci-dessus, la plage indique une variabilité des données beaucoup plus importante qu’elle ne l’est en réalité. Bien que nous ayons une grande plage, la plupart des valeurs sont en fait regroupées autour d’un milieu clair.
Parce que seuls deux nombres sont utilisés, la plage est facilement influencée par les valeurs aberrantes. Elle ne peut pas vous renseigner sur la forme de la distribution des valeurs à elle seule.
Pour avoir une idée claire de la variabilité de vos données, il est préférable d’utiliser l’étendue en combinaison avec d’autres mesures de variabilité comme l’écart interquartile et l’écart type.
Questions fréquentes sur l’étendue
En statistiques, l’étendue est la dispersion de vos données de la valeur la plus basse à la valeur la plus élevée de la distribution. C’est la mesure la plus simple de la variabilité.
Non. Comme la formule de l’étendue soustrait le nombre le plus faible du nombre le plus élevé, l’étendue est toujours nulle ou un nombre positif.
La variabilité est le plus souvent mesurée avec les statistiques descriptives suivantes :
- Etendue : la différence entre les valeurs les plus élevées et les plus basses
- Etendue interquartile : l’étendue de la moitié médiane d’une distribution
- Écart-type : distance moyenne par rapport à la moyenne
- Variance : moyenne des distances au carré par rapport à la moyenne
Alors que la tendance centrale vous indique où se situent la plupart de vos points de données, la variabilité résume la distance qui sépare vos points les uns des autres.
Des ensembles de données peuvent avoir la même tendance centrale mais différents niveaux de variabilité ou vice versa. Ensemble, ils vous donnent une image complète de vos données.

0 commentaire