|
Par définition, la pente ou l’inclinaison d’une ligne décrit sa raideur, son inclinaison ou sa déclivité.
Où
m – pente
θ – angle d’inclinaison |
 |

Si les 2 points sont connus
Si 1 point et la pente sont connus
Pente, parfois appelée gradient en mathématiques, est un nombre qui mesure la raideur et la direction d’une ligne, ou d’une section de ligne reliant deux points, et est généralement notée par m. En général, l’inclinaison d’une ligne est mesurée par la valeur absolue de sa pente, m. Plus cette valeur est grande, plus la ligne est inclinée. Étant donné m, il est possible de déterminer la direction de la ligne que m décrit en se basant sur son signe et sa valeur :
- Une ligne est croissante, et va vers le haut de gauche à droite quand m > 0
- Une ligne est décroissante, et va vers le bas de gauche à droite quand m < 0
- Une ligne a une pente constante, et est horizontale lorsque m = 0
- Une ligne verticale a une pente indéfinie, car elle donnerait lieu à une fraction dont le dénominateur serait 0. Reportez-vous à l’équation fournie ci-dessous.
La pente est essentiellement la variation de la hauteur sur la variation de la distance horizontale, et est souvent appelée « montée sur descente ». Elle a des applications dans les gradients en géographie ainsi que dans le génie civil, comme la construction de routes. Dans le cas d’une route, la « montée » est le changement d’altitude, tandis que la « descente » est la différence de distance entre deux points fixes, tant que la distance à mesurer n’est pas suffisamment grande pour que la courbure de la terre soit considérée comme un facteur. La pente est représentée mathématiquement comme suit :
| m = |
y2 – y1 |
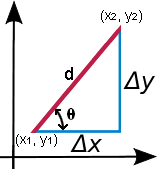
Dans l’équation ci-dessus, y2 – y1 = Δy, ou variation verticale, tandis que x2 – x1 = Δx, ou variation horizontale, comme le montre le graphique fourni. On peut également voir que Δx et Δy sont des segments de droite qui forment un triangle rectangle avec une hypoténuse d, d étant la distance entre les points (x1, y1) et (x2, y2). Puisque Δx et Δy forment un triangle rectangle, il est possible de calculer d en utilisant le théorème de Pythagore. Reportez-vous à la calculatrice des triangles pour plus de détails sur le théorème de Pythagore ainsi que sur la façon de calculer l’angle d’inclinaison θ fourni dans la calculatrice ci-dessus. Brièvement :
d = √(x2 – x1)2 + (y2 – y1)2
L’équation ci-dessus est le théorème de Pythagore à sa racine, où l’hypoténuse d a déjà été résolue, et les deux autres côtés du triangle sont déterminés en soustrayant les deux valeurs x et y données par deux points. Étant donné deux points, il est possible de trouver θ en utilisant l’équation suivante :
m = tan(θ)
Donné les points (3,4) et (6,8), trouvez la pente de la droite, la distance entre les deux points et l’angle d’inclinaison :
| m = |
8 – 4 |
= |
d = √(6 – 3)2 + (8 – 4)2 = 5
| = tan(θ) |
| θ = tan-1( | ) = 53.13° |
Bien que cela dépasse le cadre de cette calculatrice, en dehors de son utilisation linéaire de base, le concept de pente est important en calcul différentiel. Pour les fonctions non linéaires, le taux de changement d’une courbe varie, et la dérivée d’une fonction en un point donné est le taux de changement de la fonction, représenté par la pente de la ligne tangente à la courbe en ce point.
0 commentaire