Que sont les étirements et les rétrécissements horizontaux ?
Les étirements et les rétrécissements horizontaux, respectivement, tirent horizontalement le graphique de base, ou le repoussent, tout en laissant l’ordonnée à l’origine inchangée pour ancrer le graphique.
Définition
Pour la fonction de base f (x) et une constante k, où k > 0 et k ≠ 1, la fonction donnée par
g(x) = f (kx),
peut être esquissée en rétrécissant horizontalement f (x) d’un facteur de 1/k si k > 1
ou
en étirant horizontalement f (x) par un facteur de 1/k
si 0 < k < 1.
Un étirement ou un rétrécissement horizontal d’un facteur 1/k signifie que le point (x, y) du graphique de f(x) se transforme en point (x/k, y) du graphique de g(x).
Exemples d’étirements et de rétrécissements horizontaux
Considérons les fonctions de base suivantes,
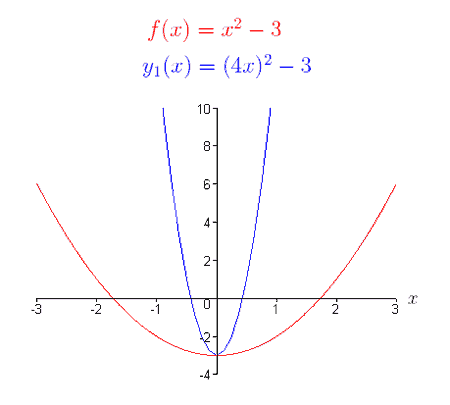
(1) f (x) = x2 – 3,
(2) g(x) = cos (x).
La représentation graphique de la fonction (1), f (x), est une parabole. À quoi ressemble, selon vous, le graphique de
y1(x) = f (4x)
? En utilisant la définition de f (x), on peut écrire y1(x) comme,
y1(x) = f (4x) = (4x)2 – 3 = 16×2-3.
Selon la définition du rétrécissement horizontal, le graphique de y1(x) devrait ressembler au graphique de
f (x), rétréci horizontalement par un facteur 1/4. Regardez les graphes de f (x) et de y1(x).
La fonction (2), g (x), est une fonction cosinus. À quoi ressemblerait le graphique de
y2(x) = g(2/3x)
? En utilisant nos connaissances sur les étirements horizontaux, le graphique de y2(x) devrait ressembler au graphique de base g(x) étiré horizontalement par un facteur 3/2. Pour vérifier cela, nous pouvons écrire y2(x) sous la forme,
y2(x) = g(2/3x) = cos (2/3x),
construire un tableau de valeurs, et tracer le graphique de la nouvelle fonction. Comme vous pouvez le constater, le graphique de y2(x) est en fait le graphique de base g(x) étiré horizontalement par un facteur 3/2.

.
0 commentaire